题目内容
8.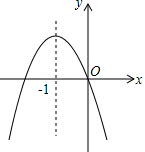 二次函数y=ax2+bx+c的图象如图所示,下列结论:①a+b+c>0;②a-b+c>0;③abc<0;④2a-b=0,其中正确的个数是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:①a+b+c>0;②a-b+c>0;③abc<0;④2a-b=0,其中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线中自变量x=1及x=-1的情况进行推理,进而对所得结论进行判断.
解答 解:①当x=1时,y=a+b+c<0,错误;
②当x=-1时,y=a-b+c>0,正确;
③由抛物线与y轴的交点为在y轴原点,c=0,因此abc=0,错误;
④∵对称轴为x=-$\frac{b}{2a}$=-1,得2a-b=0,正确;
故选B.
点评 本题主要考查图象与二次函数系数之间的关系,重点是从图象中找出重要信息.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列从左到右的变形是因式分解的是( )
| A. | (2x+1)(2x-1)=4x2-1 | B. | a2-3a-4=a(a-3)-4 | C. | 8x5y2=4x3y2•2x2 | D. | m(n-1)-(n-1)=(m-1)(n-1) |
 如图,铅球投掷场地呈扇形,其中投掷区的角度为40°,则这个角的余角为50°,补角为140°.
如图,铅球投掷场地呈扇形,其中投掷区的角度为40°,则这个角的余角为50°,补角为140°. 如图,∠DEB=∠ACB=Rt∠,DE=2,AB=5,BC=3,BD=2.5,求证:AB平分∠DBC.
如图,∠DEB=∠ACB=Rt∠,DE=2,AB=5,BC=3,BD=2.5,求证:AB平分∠DBC.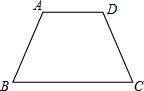 如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=7,BC=12,求∠B的度数.
如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=7,BC=12,求∠B的度数.