题目内容
20.抛物线y=-x2+(m-1)x+m.(1)求证:无论m为何值,这条抛物线都与x轴至少有一个交点;
(2)求它与x轴交点坐标A,B和与y轴的交点C的坐标;(用含m的代数式表示点坐标)
(3)S△ABC=3,求抛物线的解析式.
分析 (1)先列出三角形的代数式,然后利用配方法证明△≥0即可;
(2)令x=0可求得点C的坐标,令y=0求得方程的解,从而可求得点A、B的坐标;
(3)利用三角形的面积求得m的值从而可求得抛物线的解析式.
解答 解:(1)∵△=(m-1)2-4×1×m=(m+1)2≥0
∴无论m为何值这条抛物线都与x轴至少有一个交点;
(2)∵令x=0得:y=m,
∴点C的坐标为(0,m).
∵令y=0得;-x2+(m-1)x+m=0,解得:x=-1或x=m,
∴A(-1,0)B(m,0).
(3)由上题可得|AB|=|m+1|,OC=|m|,
∵SS△ABC=3,
∴|m+1||m|=6.
解得:m=-3,m=2.
∴y=-x2-4x-3或y=-x2+x+2.
点评 本题主要考查的是抛物线与x轴的交点,由-x2+(m-1)x+m=0解得x=-1或x=m是解题的关键.

练习册系列答案
相关题目
5.下列分式$\frac{1}{{(x-1{)^2}}}$,$\frac{1}{{{x^2}+1}}$,$\frac{5}{x-1}$的最简公分母为( )
| A. | (x2+1)(x-1) | B. | (x-1)2 | C. | (x-1)2(x2+1) | D. | (x2-1)(x2+1) |
12. 如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )
如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )
 如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )
如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )| A. | 12 | B. | 16 | C. | 24 | D. | 36 |
9.计算$\sqrt{16}$的平方根结果是( )
| A. | ±2 | B. | ±4 | C. | 2 | D. | 4 |
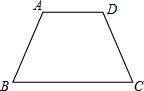 如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=7,BC=12,求∠B的度数.
如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=7,BC=12,求∠B的度数.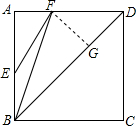 已知:如图,E、F分别是正方形ABCD的边AB和AD上的点,且$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$.求证:∠AEF=∠FBD.
已知:如图,E、F分别是正方形ABCD的边AB和AD上的点,且$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$.求证:∠AEF=∠FBD.