题目内容
4.一个圆柱的轴截面平行于投影面,圆柱的正投影是邻边长分别为4cm,3cm的矩形,求圆柱的表面积和体积.分析 根据平行投影的性质得出①当圆柱底面圆的半径为1.5cm,高为4cm,②当圆柱底面圆的半径为2cm,高为3cm,进而分别求出其表面积和体积即可.
解答 解:∵一个圆柱的轴截面平行于投影面,圆柱的正投影是邻边长分别为4cm,3cm的矩形,
∴①当圆柱底面圆的半径为1.5cm,高为4cm,
则圆柱的表面积为:2π×$\frac{3}{2}$×4+2π($\frac{3}{2}$)2=12π+$\frac{9}{2}$π=$\frac{33}{2}$π(cm2),
体积为:π($\frac{3}{2}$)2×4=9π(cm3);
②当圆柱底面圆的半径为2cm,高为3cm
则圆柱的表面积为:2π×2×3+2π×22=12π+8π=20π(cm2),
体积为:π×22×3=12π(cm3).
点评 此题主要考查了平行投影以及圆柱体的体积公式与表面积公式,得出圆柱体的底面圆的半径结合分类讨论求出答案是解题关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
15.正三角形ABC的内切圆半径为1,则△ABC的边长是( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 4 |
19.下列从左到右的变形是因式分解的是( )
| A. | (2x+1)(2x-1)=4x2-1 | B. | a2-3a-4=a(a-3)-4 | C. | 8x5y2=4x3y2•2x2 | D. | m(n-1)-(n-1)=(m-1)(n-1) |
 如图,铅球投掷场地呈扇形,其中投掷区的角度为40°,则这个角的余角为50°,补角为140°.
如图,铅球投掷场地呈扇形,其中投掷区的角度为40°,则这个角的余角为50°,补角为140°.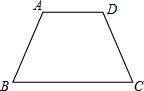 如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=7,BC=12,求∠B的度数.
如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=7,BC=12,求∠B的度数.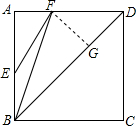 已知:如图,E、F分别是正方形ABCD的边AB和AD上的点,且$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$.求证:∠AEF=∠FBD.
已知:如图,E、F分别是正方形ABCD的边AB和AD上的点,且$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$.求证:∠AEF=∠FBD.