题目内容
16.已知一个圆心角为270°、半圆的半径为3m的扇形工件,未搬动前如图所示,A、B两点触地放置,搬动时,先将扇形以B为圆心,作如图所示的无滑动翻转,再使它紧贴地面滚动,当A、B两点再次触地时算一次,则n次滚动以后,圆心O所经过的路线长是6nπm.(结果用含π的式子表示)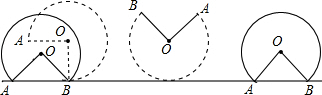
分析 O经过的路线是两个半径是3,圆心角为45°的弧,平移的距离是半径为3,圆心角是270°的弧长,二者的和就是所求的一次的路线长,再乘以n即可.
解答 解:∠AOB=360°-270°=90°,则∠ABO=45°,
则∠OBC=45°,
O旋转的长度是:2×$\frac{45π×3}{180}$=$\frac{3π}{2}$;
O移动的距离是:$\frac{270π×3}{180}$=$\frac{9π}{2}$,
则圆心O所经过的路线长是:$\frac{3π}{2}$+$\frac{9π}{2}$=6π,
则n次滚动以后,圆心O所经过的路线长是6π×n=6nπ,
故答案为:6nπ.
点评 本题考查了弧长的计算公式,正确理解O经过的路线是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列命题是假命题的是( )
| A. | 若a2=b2,则a=b | |
| B. | 两直线平行,同位角相等 | |
| C. | 对顶角相等 | |
| D. | 若b2-4ac>0,则方程ax2+bx+c=0(a≠0)有两个不等的实数根 |
8.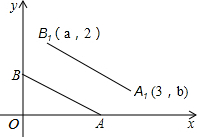 如图,平面直角坐标系中,A、B两点的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,则a,b的值分别为( )
如图,平面直角坐标系中,A、B两点的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,则a,b的值分别为( )
 如图,平面直角坐标系中,A、B两点的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,则a,b的值分别为( )
如图,平面直角坐标系中,A、B两点的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,则a,b的值分别为( )| A. | 1,3 | B. | 1,2 | C. | 2,1 | D. | 1,1 |

