题目内容
7.已知不等式组$\left\{\begin{array}{l}{(x+1)(x-3)>x(x-5)}\\{\frac{x}{2}<1-a}\end{array}\right.$无解,则a的取值范围是a≥$\frac{1}{2}$.分析 先求出每个不等式的解集,再根据已知得出关于a的不等式,求出不等式的解集即可.
解答 解:$\left\{\begin{array}{l}{(x+1)(x-3)>x(x-5)①}\\{\frac{x}{2}<1-a②}\end{array}\right.$
∵解不等式①得:x>1,
解不等式②得:x<2-2a,
又∵不等式组$\left\{\begin{array}{l}{(x+1)(x-3)>x(x-5)}\\{\frac{x}{2}<1-a}\end{array}\right.$无解,
∴1≥2-2a,
解得:a≥$\frac{1}{2}$,
故答案为:a≥$\frac{1}{2}$.
点评 本题考查了解一元一次不等式(组)的应用,解此题的关键是能得出关于a的不等式.

练习册系列答案
相关题目
15. 如图,E是正方形ABCD边AB延长线上一点,且BD=BE,则∠BED的大小为( )
如图,E是正方形ABCD边AB延长线上一点,且BD=BE,则∠BED的大小为( )
 如图,E是正方形ABCD边AB延长线上一点,且BD=BE,则∠BED的大小为( )
如图,E是正方形ABCD边AB延长线上一点,且BD=BE,则∠BED的大小为( )| A. | 15° | B. | 22.5° | C. | 30° | D. | 45° |
12.下列各式中,正确的是( )
| A. | $\root{3}{-5}$=-$\root{3}{5}$ | B. | $\sqrt{16}$=±4 | C. | $\sqrt{(-13)^{2}}$=-13 | D. | $\sqrt{3.6}$=0.6 |
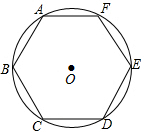 如图,已知正六边形ABCDEF没接于半径为4的⊙O,则B、D两点间的距离为4$\sqrt{3}$.
如图,已知正六边形ABCDEF没接于半径为4的⊙O,则B、D两点间的距离为4$\sqrt{3}$.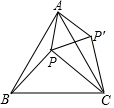 如图,点P是等边△ABC内一点,连接PA,PB,PC,PA:PB:PC=3:4:5,以AC为边作△AP′C≌△APB,连接PP′,则有以下结论:①△APP′是等边三角形;②△PCP′是直角三角形;③∠APB=150°;④∠APC=105°.其中一定正确的是①②③.(把所有正确答案的序号都填在横线上)
如图,点P是等边△ABC内一点,连接PA,PB,PC,PA:PB:PC=3:4:5,以AC为边作△AP′C≌△APB,连接PP′,则有以下结论:①△APP′是等边三角形;②△PCP′是直角三角形;③∠APB=150°;④∠APC=105°.其中一定正确的是①②③.(把所有正确答案的序号都填在横线上)
 如图,菱形ABCD边长为9,DF交AC于点E,且AE=AF=6,则EF的长为2$\sqrt{3}$.
如图,菱形ABCD边长为9,DF交AC于点E,且AE=AF=6,则EF的长为2$\sqrt{3}$.