题目内容
18．先化简，再求值：$\frac{x-2}{{x}^{2}-1}$÷（x-1-$\frac{2x-1}{x+1}$），其中x是方程x2+x-6=0的根．分析 先根据分式混合运算的法则把原式进行化简，再求出x的值代入进行计算即可．
解答 解：原式=$\frac{x-2}{（x+1）（x-1）}$÷$\frac{（x+1）（x-1）-2x+1}{x+1}$
=$\frac{x-2}{（x+1）（x-1）}$•$\frac{x+1}{x（x-2）}$
=$\frac{1}{x（x-1）}$，
由x2+x-6=0，得x=-3或x=2（原分式无意义，舍去），
则当x=-3时，原式=$\frac{1}{12}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
全能测控期末小状元系列答案
相关题目
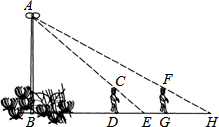如图，花丛中有一路灯杆AB，在灯光下，大华在D点处的影长DE=3米，沿BD方向行走到达G点，DG=5米，这时大华的影长GH=5米．如果大华的身高为2米，求路灯杆AB的高度．
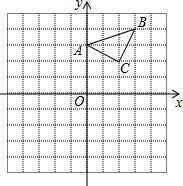已知：在平面直角坐标系中，△ABC三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）．（正方形网格中，每个小正方形的边长是1个单位长度）
3．下列命题为假命题的是（ ）
| A． | 对顶角相等 | B． | 两直线平行，同位角相等 | ||
| C． | 内错角相等 | D． | 三角形内角和是180度 |
7．在平面直角坐标系中，点A（-2，3）关于y轴对称的点A′的坐标是（ ）
| A． | （-2，6） | B． | （2，3） | C． | （-2，-3） | D． | （2，-3） |
