题目内容
10．甲、乙、丙三人相互传球，由乙开始发球，并作为第一次传球．用列表或画树状图的方法求经过3次传球后，球仍回到乙手中的概率．分析 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与经过3次传球后，球仍回到乙手中的情况，再利用概率公式求解即可求得答案．
解答 解：（1）画树状图得：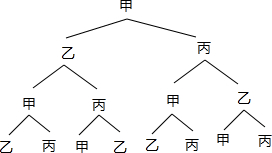
∵共有8种等可能的结果，经过3次传球后，球仍回到乙手中的有2种情况，
∴经过3次传球后，球仍回到乙手中的概率是：$\frac{2}{8}$=$\frac{1}{4}$．
点评 本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．注意概率=所求情况数与总情况数之比．
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
为了预防“流感”，某学校对教室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y（mg）与时间x（min）成正比例，药物燃烧完后，y与x成反比例（如图所示）．现测得药物8min燃毕，此时室内空气中每立方米的含药量为6mg．研究表明，当空气中每立方米的含药量不低于3mg才有效，那么此次消毒的有效时间是多少？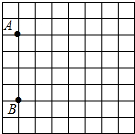
有一张图纸被损坏，但上面有如图所示的两个标志点A（-3，1），B（-3，-3）可见，而主要建筑C（3，2）破损，
15．函数$y=\frac{{\sqrt{x-2}}}{x-4}$的自变量的取值范围是（ ）
| A． | x≥2 | B． | x≥2且x≠4 | C． | x＞2且x≠4 | D． | x≠4 |