题目内容
13.有六张正面分别标有数字-2、-1、0、1、2、3的卡片,除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽取一张,记下卡片上的数字为a,则关于x的不等式组$\left\{\begin{array}{l}x+1≥2\\ x-m≤0\end{array}\right.$有解,且分式方程$\frac{m}{x-2}=\frac{1}{x+2}$有整数解的概率是$\frac{1}{6}$.分析 根据不等式组的解集及分式方程有解求出m的取值范围,再根据概率公式即可得出答案.
解答 解:由关于x的不等式组$\left\{\begin{array}{l}x+1≥2\\ x-m≤0\end{array}\right.$有解,且分式方程$\frac{m}{x-2}=\frac{1}{x+2}$有整数解,得
1≤x≤m且x=$\frac{-2m-2}{m-2}$是整数,得
m=3.
∴符合条件的m的值是3,
∴关于x的不等式组$\left\{\begin{array}{l}x+1≥2\\ x-m≤0\end{array}\right.$有解,且分式方程$\frac{m}{x-2}=\frac{1}{x+2}$有整数解的概率是$\frac{1}{6}$,
故答案为:$\frac{1}{6}$.
点评 此题考查了概率公式,用到的知识点是不等式组、分式方程和概率=所求情况数与总情况数之比.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
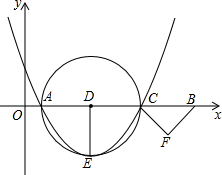 如图,在平面直角坐标系中,点A(1,0)、B(11,0),点C为线段AB上一动点,以AC为直径的⊙D的半径DE⊥AC,△CBF是以CB为斜边的等腰直角三角形,且点E、F都在第四象限,当点F到过点A、C、E三点的抛物线的顶点的距离最小时,该抛物线的解析式为y=$\frac{2}{5}$(x-$\frac{7}{2}$)2-$\frac{5}{2}$.
如图,在平面直角坐标系中,点A(1,0)、B(11,0),点C为线段AB上一动点,以AC为直径的⊙D的半径DE⊥AC,△CBF是以CB为斜边的等腰直角三角形,且点E、F都在第四象限,当点F到过点A、C、E三点的抛物线的顶点的距离最小时,该抛物线的解析式为y=$\frac{2}{5}$(x-$\frac{7}{2}$)2-$\frac{5}{2}$.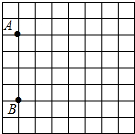 有一张图纸被损坏,但上面有如图所示的两个标志点A(-3,1),B(-3,-3)可见,而主要建筑C(3,2)破损,
有一张图纸被损坏,但上面有如图所示的两个标志点A(-3,1),B(-3,-3)可见,而主要建筑C(3,2)破损,