题目内容
9.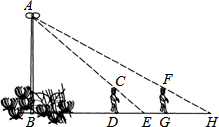 如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
分析 根据相似三角形的判定,由CD∥AB得△EAB∽△ECD,利用相似比有$\frac{2}{AB}$=$\frac{3}{3+BD}$,同理可得$\frac{2}{AB}$=$\frac{5}{BD+5+5}$,然后解关于AB和BD的方程组求出AB即可.
解答 解:∵CD∥AB,
∴△EAB∽△ECD,
∴$\frac{CD}{AB}$=$\frac{DE}{BE}$,即$\frac{2}{AB}$=$\frac{3}{3+BD}$①,
∵FG∥AB,
∴△HFG∽△HAB,
∴$\frac{FG}{AB}$=$\frac{HG}{HB}$,即$\frac{2}{AB}$=$\frac{5}{BD+5+5}$②,
由①②得$\frac{3}{3+BD}$=$\frac{5}{BD+5+5}$,
解得BD=7.5,
∴$\frac{2}{AB}$=$\frac{3}{7.5+3}$,解得:AB=7.
答:路灯杆AB的高度为7m.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.

练习册系列答案
相关题目
17.若两个相似三角形的周长比为1:3,则面积比为( )
| A. | 1:3 | B. | 3:1 | C. | 1:9 | D. | 9:1 |
 如图,∠ABC=∠DCB=90°,且AC=BD.AB与DC相等吗?∠BAC与∠CDB相等吗?为什么?
如图,∠ABC=∠DCB=90°,且AC=BD.AB与DC相等吗?∠BAC与∠CDB相等吗?为什么? 为了预防“流感”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例(如图所示).现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg.研究表明,当空气中每立方米的含药量不低于3mg才有效,那么此次消毒的有效时间是多少?
为了预防“流感”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例(如图所示).现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg.研究表明,当空气中每立方米的含药量不低于3mg才有效,那么此次消毒的有效时间是多少?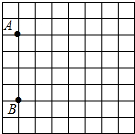 有一张图纸被损坏,但上面有如图所示的两个标志点A(-3,1),B(-3,-3)可见,而主要建筑C(3,2)破损,
有一张图纸被损坏,但上面有如图所示的两个标志点A(-3,1),B(-3,-3)可见,而主要建筑C(3,2)破损,