题目内容
12.计算:(1)$({\sqrt{24}-\sqrt{2}})-({\sqrt{8}+\sqrt{6}})$;
(2)${(2-\sqrt{3})^{2013}}•{(2+\sqrt{3})^{2014}}-2|{-\frac{{\sqrt{3}}}{2}}|-{(-\sqrt{3})^0}$
(3)$({\sqrt{6}+\sqrt{2}})({\sqrt{6}-\sqrt{2}})$
(4)$({2\sqrt{48}-3\sqrt{27}})÷\sqrt{6}$
(5)$(\sqrt{48}-4\sqrt{\frac{1}{8}})-(3\sqrt{\frac{1}{3}}-2\sqrt{0.5})$
(6)$\sqrt{8}×\sqrt{\frac{1}{2}}+{(\sqrt{2})^0}$.
分析 (1)先化简二次根式,然后合并二次根式;
(2)根据同底数幂的乘法和积的乘方、绝对值的性质以及零指数的意义进行计算,求出即可.
(3)利用乘法公式计算;
(4)根据多项式除以单项式的法则进行计算;
(5)去括号,化简二次根式,然后合并二次根式;
(6)根据混合运算的顺序进行计算.
解答 解:
(1)$({\sqrt{24}-\sqrt{2}})-({\sqrt{8}+\sqrt{6}})$
=2$\sqrt{6}$-$\sqrt{2}$-2$\sqrt{2}$-$\sqrt{6}$
=$\sqrt{6}$-3$\sqrt{2}$;
(2)${(2-\sqrt{3})^{2013}}•{(2+\sqrt{3})^{2014}}-2|{-\frac{{\sqrt{3}}}{2}}|-{(-\sqrt{3})^0}$
=[(2-$\sqrt{3}$)(2+$\sqrt{3}$)]2013(2+$\sqrt{3}$)-$\sqrt{3}$-1
=2+$\sqrt{3}$-$\sqrt{3}$-1
=1;
(3)$({\sqrt{6}+\sqrt{2}})({\sqrt{6}-\sqrt{2}})$
=6-2
=4;
(4)$({2\sqrt{48}-3\sqrt{27}})÷\sqrt{6}$
=4$\sqrt{2}$-$\frac{9}{2}$$\sqrt{2}$
=-$\frac{\sqrt{2}}{2}$;
(5)$(\sqrt{48}-4\sqrt{\frac{1}{8}})-(3\sqrt{\frac{1}{3}}-2\sqrt{0.5})$
=4$\sqrt{3}$-$\sqrt{2}$-$\sqrt{3}$+$\sqrt{2}$
=3$\sqrt{3}$;
(6)$\sqrt{8}×\sqrt{\frac{1}{2}}+{(\sqrt{2})^0}$
=2+1
=3.
点评 本题考查了二次根式的混合运算,熟练掌握混合运算的法则是解题的关键.

 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案| A. | 6 | B. | -8 | C. | $\frac{1}{8}$ | D. | $-\frac{1}{8}$ |
 如图,在三角形ABC中,AB∥DE,AD⊥BC,∠BAC=90°,与∠DAC相等的角(不包括∠DAC本身)有( )
如图,在三角形ABC中,AB∥DE,AD⊥BC,∠BAC=90°,与∠DAC相等的角(不包括∠DAC本身)有( )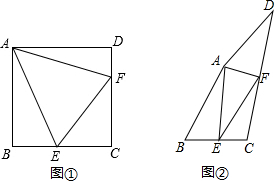
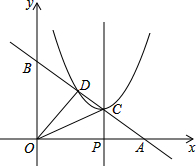 已知直线y=-$\frac{3}{4}x+3$分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒,以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D,设△COD的OC边上的高为h,当t=$\frac{36}{25}$时,h的值最大.
已知直线y=-$\frac{3}{4}x+3$分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒,以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D,设△COD的OC边上的高为h,当t=$\frac{36}{25}$时,h的值最大.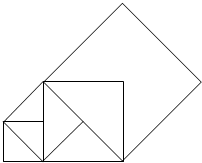 如图,先画一个边长为1的正方形,以其对角线为边画第二个正方形,再以第二个正方形的对角线为边画第三个正方形,…,如此反复下去,那么第n个正方形的对角线长为($\sqrt{2}$)n.
如图,先画一个边长为1的正方形,以其对角线为边画第二个正方形,再以第二个正方形的对角线为边画第三个正方形,…,如此反复下去,那么第n个正方形的对角线长为($\sqrt{2}$)n.