题目内容
16. 我国古算书《九章算术》中有“圆材埋壁”一题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径(直径)几何?”(注:如图,⊙O表示圆材截面,CE是⊙O的直径,AB表示“锯道”,CD表示“锯深”,1尺=10寸,求圆材的直径长就是求CE的长.)
我国古算书《九章算术》中有“圆材埋壁”一题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径(直径)几何?”(注:如图,⊙O表示圆材截面,CE是⊙O的直径,AB表示“锯道”,CD表示“锯深”,1尺=10寸,求圆材的直径长就是求CE的长.)
分析 由垂径定理得出AD=5,勾股定理OA2=OD2+AD2,代入数据求得OA,即可得出直径.
解答 解:连接OA,如图所示:
∵AB⊥CE,
∴AD=BD,
∵AB=10,
∴AD=5,
在Rt△AOE中,∵OA2=OD2+AD2,
∴OA2=(OA-1)2+52,
解得:OA=13,
∴CD=2A0=26;
即直径为26寸.
点评 本题考查了垂径定理、勾股定理的综合运用;熟练掌握垂径定理,由勾股定理求出OA是解决问题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0;②b+2a=0;③ac<$\frac{1}{4}$b2;④3a+c>0.其中正确的命题是②③.
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0;②b+2a=0;③ac<$\frac{1}{4}$b2;④3a+c>0.其中正确的命题是②③. 在Rt△ABC中,∠A=90°,
在Rt△ABC中,∠A=90°,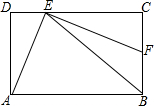 如图,在矩形ABCD中,BE平分∠ABC且交CD于点E,EF⊥AE且交BC于点F,求证:AE=EF.
如图,在矩形ABCD中,BE平分∠ABC且交CD于点E,EF⊥AE且交BC于点F,求证:AE=EF. 如图,AB是⊙O的直径,CD是⊙O的弦,求证:AE•BC=AD•CE.
如图,AB是⊙O的直径,CD是⊙O的弦,求证:AE•BC=AD•CE.