题目内容
2. 如图,MN是⊙O的直径,MN=2,点A在圆周上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则△PAB周长的最小值为( )
如图,MN是⊙O的直径,MN=2,点A在圆周上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则△PAB周长的最小值为( )| A. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | B. | $\frac{1}{2}$+$\sqrt{2}$ | C. | $\frac{\sqrt{3}+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ |
分析 作AE⊥MN交⊙O于E,连接BE交MN于点P作AF⊥OB于F,连接AP,此时△PAB周长最小,因为△APB周长=AP+PB+AB=PE+PB+AB=BE+AB,只要求出AB,BE即可.
解答 解:作AE⊥MN交⊙O于E,连接BE交MN于点P作AF⊥OB于F,连接AP,此时△PAB周长最小.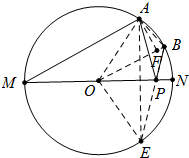
∵MN是直径,AE⊥MN,
∴$\widehat{AN}$=$\widehat{EN}$,
∵∠M=30°,
∴∠AON=∠NOE=60°,
∵$\widehat{AB}$=$\widehat{BN}$,
∴∠AOB=∠BON=30°,
在RT△AOF中,∠AFO=90°,AO=1,
∴AF=$\frac{1}{2}$AO=$\frac{1}{2}$,OF=$\frac{\sqrt{3}}{2}$,FB=1-$\frac{\sqrt{3}}{2}$,
∴AB=$\sqrt{A{F}^{2}+B{F}^{2}}$=$\sqrt{(\frac{1}{2})^{2}+(1-\frac{\sqrt{3}}{2})^{2}}$=$\frac{1}{2}$($\sqrt{6}$-$\sqrt{2}$),
∵∠BOE=∠BON+∠NOE=90°,
∴BE=$\sqrt{2}$,
∴△APB周长=AP+PB+AB=PE+PB+AB=BE+AB=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
故选A.
点评 本题考查轴对称-最短问题、圆的有关知识、勾股定理、两点之间线段最短等知识,解题的关键是利用对称变换找到点P,属于中考常考题型.

练习册系列答案
相关题目
17.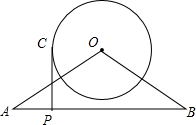 如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )
如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )
 如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )
如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )| A. | 3≤PC≤3$\sqrt{17}$ | B. | 5≤PC≤13 | C. | 4≤PC≤3$\sqrt{17}$ | D. | 1<PC≤13 |
3.点O是矩形ABCD内任意一点,点O到点A、B、C的距离分别为a、b、c,那么点O到点D的距离为( )
| A. | $\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}$ | B. | $\sqrt{{a}^{2}-{b}^{2}-{c}^{2}}$ | C. | $\sqrt{{a}^{2}-{b}^{2}+{c}^{2}}$ | D. | $\sqrt{-{c}^{2}+{b}^{2}+{a}^{2}}$ |
 如图,点M、N分别在直线a、b上,且a∥b,P为两平行线间一点,那么∠1+∠2+∠3=360°.
如图,点M、N分别在直线a、b上,且a∥b,P为两平行线间一点,那么∠1+∠2+∠3=360°. 如图,一次函数y1=k1x+b(k1>0)的图象经过点C(-3,0),且与两坐标轴围成的三角形的面积为3.
如图,一次函数y1=k1x+b(k1>0)的图象经过点C(-3,0),且与两坐标轴围成的三角形的面积为3.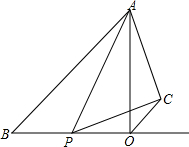 在Rt△AOB中,∠AOB=90°,OA=OB=4厘米,点P从B出发,以1厘米/秒的速度沿射线BO运动,设点P运动时间为t(t>0)秒.△APC是以AP为斜边的等腰直角三角形,且C,O两点在直线AB的同侧,连接OC.
在Rt△AOB中,∠AOB=90°,OA=OB=4厘米,点P从B出发,以1厘米/秒的速度沿射线BO运动,设点P运动时间为t(t>0)秒.△APC是以AP为斜边的等腰直角三角形,且C,O两点在直线AB的同侧,连接OC.