题目内容
4.已知平面直角坐标系中有两点M(-2,3)、N(4,1),点P在x轴上,当MP+NP最小时,P的坐标是($\frac{5}{2}$,0).分析 作点N关于x轴的对称点E(4,-1),连接ME与x轴的交点就是所求的点P,求出直线ME与x轴的交点即可.
解答 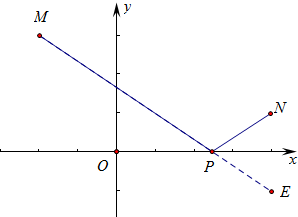 解:如图作点N关于x轴的对称点E(4,-1),连接ME与x轴的交点就是所求的点P.
解:如图作点N关于x轴的对称点E(4,-1),连接ME与x轴的交点就是所求的点P.
设直线ME为y=kx+b,把M(-2,3),E(4,-1)代入得$\left\{\begin{array}{l}{-2k+b=3}\\{4k+b=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{2}{3}}\\{b=\frac{5}{3}}\end{array}\right.$,
∴直线EM为y=-$\frac{2}{3}$x+$\frac{5}{3}$,令y=0,则x=$\frac{5}{2}$,
∴点P坐标($\frac{5}{2}$,0).
故答案为($\frac{5}{2}$,0).
点评 本题考查轴对称-最短问题、坐标与图形性质、一次函数等知识,解题的关键是利用轴对称找到点P位置,利用一次函数解决于x轴交点问题,属于中考常考题型.

练习册系列答案
相关题目
2. 如图,MN是⊙O的直径,MN=2,点A在圆周上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则△PAB周长的最小值为( )
如图,MN是⊙O的直径,MN=2,点A在圆周上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则△PAB周长的最小值为( )
 如图,MN是⊙O的直径,MN=2,点A在圆周上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则△PAB周长的最小值为( )
如图,MN是⊙O的直径,MN=2,点A在圆周上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则△PAB周长的最小值为( )| A. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | B. | $\frac{1}{2}$+$\sqrt{2}$ | C. | $\frac{\sqrt{3}+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ |
13.在平面直角坐标系中,点A到x轴的距离为1,到y轴的距离为2.若点A在第二象限,则A点坐标为( )
| A. | (-1,2) | B. | (2,-1) | C. | (-2,1) | D. | (2,1) |
 如图,在方格纸中有三个点A、B、C,若点A的位置记为(0,1),点B的位置记为(2,-1),则点C的位置应记为(-3,-2).
如图,在方格纸中有三个点A、B、C,若点A的位置记为(0,1),点B的位置记为(2,-1),则点C的位置应记为(-3,-2). 如图为某战役缴获敌人防御工事坐标地图碎片,依稀可见一号暗堡坐标为(1,2),二号暗堡坐标为(-3,2),另由情报得知,指挥部坐标为(-1,-2),你能在图上际出指挥部的位置P吗?试通过画图加以说明.
如图为某战役缴获敌人防御工事坐标地图碎片,依稀可见一号暗堡坐标为(1,2),二号暗堡坐标为(-3,2),另由情报得知,指挥部坐标为(-1,-2),你能在图上际出指挥部的位置P吗?试通过画图加以说明.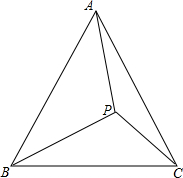 如图,在△ABC中,AB=BC,点P是△ABC内部的一点,∠BAP+∠BCP=90°,若AP=4,BP=5,CP=3,求证:△ABC为正三角形.
如图,在△ABC中,AB=BC,点P是△ABC内部的一点,∠BAP+∠BCP=90°,若AP=4,BP=5,CP=3,求证:△ABC为正三角形.