题目内容
12．已知，∠ABC=90°，∠BAC=50°，点D是直线AC上的一个动点，将三角形CDB沿着线段DB翻折，翻折后点C对应点为点E，当∠ABD=20°时，BE∥AC．分析 根据BE∥AC可以求得∠CBE的度数，然后根据BD是CE的对称轴即可求得∠CBD的度数，则∠ABD即可求得．
解答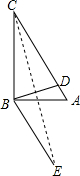 
解：直角△ABC中，∠ACB=90°-∠BAC=90°-50°=40°．
∵BE∥AC，
∴∠CBE=180°-∠BAC=180°-40°=140°，
∵C、E关于BD对称，
∴∠CBD=$\frac{1}{2}$∠CBE=$\frac{1}{2}$×140°=70°，
∴∠ABD=∠ABC-∠CBD=90°-70°=20°．
故答案是：20．
点评 本题考查了翻折变换以及平行线的性质，正确作出图形，求得∠CBD的度数是关键．
练习册系列答案
相关题目
7．若关于x的一元二次方程m2x2-（2m-1）x-1=0有两个实数根，则m的取值范围是（ ）
| A． | m$＜\frac{1}{4}$ | B． | m$≤\frac{1}{4}$ | C． | m$≥\frac{1}{4}$ | D． | m$≤\frac{1}{4}$且m≠0 |
4．
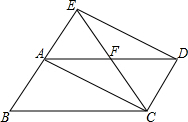如图，将平行四边形ABCD沿对角线AC折叠，点B的对应点落在点E处，且点B、A、E在同一条直线上，CE交AD于点F，连接ED．下列结论中错误的是（ ）
如图，将平行四边形ABCD沿对角线AC折叠，点B的对应点落在点E处，且点B、A、E在同一条直线上，CE交AD于点F，连接ED．下列结论中错误的是（ ）| A． | AF=$\frac{1}{2}BC$ | B． | 四边形ACDE是矩形 | ||
| C． | 图中与△ABC全等的三角形有4个 | D． | 图中有4个等腰三角形 |
2．
如图，MN是⊙O的直径，MN=2，点A在圆周上，∠AMN=30°，B为弧AN的中点，P是直径MN上一动点，则△PAB周长的最小值为（ ）
如图，MN是⊙O的直径，MN=2，点A在圆周上，∠AMN=30°，B为弧AN的中点，P是直径MN上一动点，则△PAB周长的最小值为（ ）| A． | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | B． | $\frac{1}{2}$+$\sqrt{2}$ | C． | $\frac{\sqrt{3}+\sqrt{2}}{2}$ | D． | $\frac{\sqrt{6}-\sqrt{2}}{2}$ |