��Ŀ����
4����ͼ1��2��3�ֱ��ʾ�ס��ҡ���������A�ص�B�ص�·��ͼ����֪
��·��Ϊ��A��C��B��
�ҵ�·��Ϊ��A��D��E��F��B������EΪAB���е㣻
����·��Ϊ��A��I��J��K��B������J��AB�ϣ���AJ��JB��
������[��]��ʾ[ֱ��ǰ��]�������ͼ��������ͼ���ģ���ͼ���壩�����ݣ��ж������н�·�߳��ȵĴ�С��ϵΪ��������
| A�� | ��=��=�� | B�� | �ף��ң��� | C�� | �ң������� | D�� | �����ң��� |
���� �ɽǵĶ�������֪��2��3�е����������εĶ�Ӧ�߶���ƽ�еģ�����ͼ2��ͼ3�е������ζ���ͼ1�е����������ƣ�����ͼ2������ȫ�ȣ�ͼ3����������
���  �⣺�������Ϸ���������ͼ2�ɵ�AE=BE��AD=EF��DE=BE��
�⣺�������Ϸ���������ͼ2�ɵ�AE=BE��AD=EF��DE=BE��
��AE=BE=$\frac{1}{2}$AB��
��AD=EF=$\frac{1}{2}$AC��DE=BE=$\frac{1}{2}$BC��
���=��
ͼ3��ͼ1�У��������������ƣ����� $\frac{JK}{AI}$=$\frac{JB}{AJ}$=$\frac{BK}{IJ}$��$\frac{AI}{AC}$=$\frac{AJ}{AB}$=$\frac{IJ}{BC}$��
��AJ+BJ=AB��
��AI+JK=AC��IJ+BK=BC
���=�������=��=����
��ѡA��
���� ���⿼���֪ʶ����ƽ���ı��ε����ʣ��ؼ�������Ҫ���������ε����������ε�ƽ�ƣ�������߶εĹ�ϵ��

��ϰ��ϵ�д�
 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д� Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
�����Ŀ
14��������˵�����Ǵ�����ǣ�������
| A�� | �ڡ�ABC�У�����A����B����C=5��2��3�����ABCΪֱ�������� | |
| B�� | �ڡ�ABC�У���C=��A-��B�����ABCΪֱ�������� | |
| C�� | �ڡ�ABC�У���a=$\frac{3}{5}$c��b=$\frac{4}{5}$c�����ABCΪֱ�������� | |
| D�� | �ڡ�ABC�У���a��b��c=2��2��4�����ABCΪֱ�������� |
15��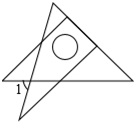 ��һ��ֱ�����ǰ���ͼ���ã�ʹ��30��ǵ����ǰ��ֱ�DZߺͺ�45��ǵ����ǰ��һ��ֱ�DZ��غϣ����1�Ķ���Ϊ��������
��һ��ֱ�����ǰ���ͼ���ã�ʹ��30��ǵ����ǰ��ֱ�DZߺͺ�45��ǵ����ǰ��һ��ֱ�DZ��غϣ����1�Ķ���Ϊ��������
 ��һ��ֱ�����ǰ���ͼ���ã�ʹ��30��ǵ����ǰ��ֱ�DZߺͺ�45��ǵ����ǰ��һ��ֱ�DZ��غϣ����1�Ķ���Ϊ��������
��һ��ֱ�����ǰ���ͼ���ã�ʹ��30��ǵ����ǰ��ֱ�DZߺͺ�45��ǵ����ǰ��һ��ֱ�DZ��غϣ����1�Ķ���Ϊ��������| A�� | 60�� | B�� | 75�� | C�� | 65�� | D�� | 70�� |
12����ʽ��$\frac{1}{x+1}$��$\frac{1}{x+2}$��$\sqrt{x+1}$��$\sqrt{x+2}$�У�x����ͬʱȡ-1��-2���ǣ�������
| A�� | $\frac{1}{x+1}$ | B�� | $\frac{1}{x+2}$ | C�� | $\sqrt{x+1}$ | D�� | $\sqrt{x+2}$ |
16���ڡ�ABC�У�����BAC=90�㣬������
| A�� | BC=AB+AC | B�� | AC2=AB2+BC2 | C�� | AB2=AC2+BC2 | D�� | BC2=AB2+AC2 |
14����bС-3�����ǣ�������
| A�� | -b+3 | B�� | b+3 | C�� | b-3 | D�� | -b-3 |

 ������ͼ��ʾ�ij�����㺯��ֵ���������x��ֵΪ$\frac{5}{2}$���������y��ֵΪ$\frac{2}{5}$��
������ͼ��ʾ�ij�����㺯��ֵ���������x��ֵΪ$\frac{5}{2}$���������y��ֵΪ$\frac{2}{5}$�� ����ͼ��ʾ�ij�����㣬����ʼ����x��ֵΪ6�����Ƿ��ֵ�һ�εõ��Ľ��Ϊ3����2�εõ��Ľ��Ϊ10����3�εõ��Ľ��Ϊ5������̽����4�εõ��Ľ��Ϊ12����2011�εõ��Ľ��Ϊ3��
����ͼ��ʾ�ij�����㣬����ʼ����x��ֵΪ6�����Ƿ��ֵ�һ�εõ��Ľ��Ϊ3����2�εõ��Ľ��Ϊ10����3�εõ��Ľ��Ϊ5������̽����4�εõ��Ľ��Ϊ12����2011�εõ��Ľ��Ϊ3��