题目内容
16．在△ABC中，若∠BAC=90°，则（ ）| A． | BC=AB+AC | B． | AC2=AB2+BC2 | C． | AB2=AC2+BC2 | D． | BC2=AB2+AC2 |
分析 在△ABC中，若∠BAC=90°，则△ABC是直角三角形，其中直角边分别为AB与AC，斜边为CB，由勾股定理即可求解．
解答 解：如图，
∵在△ABC中，∠BAC=90°，
∴BC2=AB2+AC2
故选D．
点评 本题考查了勾股定理的定义，解题的关键是掌握“直角三角形中，斜边的平方等于两直角边的平方的和”，要判定△ABC 中那个是斜边、那个是直角边．
练习册系列答案
相关题目
6．
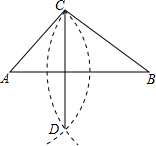已知△ABC，按如下步骤作图：
（1）以点A为圆心，以AC的长为半径画弧；
（2）以点B为圆心，以BC的长为半径画弧，与前一段弧相交于点D；
（3）连接CD，
若AC=5，BC=CD=8．则AB的长是（ ）
已知△ABC，按如下步骤作图：（1）以点A为圆心，以AC的长为半径画弧；
（2）以点B为圆心，以BC的长为半径画弧，与前一段弧相交于点D；
（3）连接CD，
若AC=5，BC=CD=8．则AB的长是（ ）
| A． | 3+2$\sqrt{3}$ | B． | 10 | C． | 3+4$\sqrt{3}$ | D． | 12 |
7．一组按规律排列的式子：a2，$\frac{{a}^{4}}{3}$，$\frac{{a}^{6}}{5}$，$\frac{{a}^{8}}{7}$，…，则第2016个式子是（ ）
| A． | $\frac{{a}^{2016}}{2015}$ | B． | $\frac{{a}^{2016}}{4029}$ | C． | $\frac{{a}^{4032}}{4031}$ | D． | $\frac{{a}^{4032}}{4029}$ |
4．如图1、2、3分别表示甲、乙、丙三人由A地到B地的路线图，已知
甲的路线为：A→C→B；
乙的路线为：A→D→E→F→B，其中E为AB的中点；
丙的路线为：A→I→J→K→B，其中J在AB上，且AJ＞JB．
若符号[→]表示[直线前进]，则根据图（三）、图（四）、图（五）的数据，判断三人行进路线长度的大小关系为（ ）
甲的路线为：A→C→B；
乙的路线为：A→D→E→F→B，其中E为AB的中点；
丙的路线为：A→I→J→K→B，其中J在AB上，且AJ＞JB．
若符号[→]表示[直线前进]，则根据图（三）、图（四）、图（五）的数据，判断三人行进路线长度的大小关系为（ ）
| A． | 甲=乙=丙 | B． | 甲＜乙＜丙 | C． | 乙＜丙＜甲 | D． | 丙＜乙＜甲 |
11．已知a-b=3，则代数式a2-b2-6b的值为（ ）
| A． | 3 | B． | 6 | C． | 9 | D． | 12 |
1．
如图，在△ABC中，∠A=50°，BD⊥AC于点D，CE⊥AB于点E，BD、CE相交于点O，则∠BOC=（ ）
如图，在△ABC中，∠A=50°，BD⊥AC于点D，CE⊥AB于点E，BD、CE相交于点O，则∠BOC=（ ）| A． | 120° | B． | 130° | C． | 140° | D． | 150° |
8．
A，B，C三个车站在东西笔直的一条公路上，现要建一个加油站使其到三个车站的距离和最小，则加油站应建在（ ）
A，B，C三个车站在东西笔直的一条公路上，现要建一个加油站使其到三个车站的距离和最小，则加油站应建在（ ）| A． | 在A的左侧 | B． | 在AB之间 | C． | 在BC之间 | D． | B处 |
在直角坐标系中，点A的坐标是（3，0），点P在第一象限内的直线y=-x+4上．设点P的坐标为（x，y）．
6．下列说法中，正确的是（ ）
| A． | 延长直线AB | B． | 在射线AM上顺次截取线段AC=CB=a | ||
| C． | 如果AC=BC，则点C为AB的中点 | D． | 平角是一条直线 |