题目内容
18.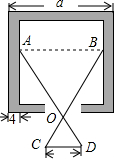 如图,若OA:OD=OB:OC=n,则x=$\frac{a-bn}{2}$.(用a,b,n表示).
如图,若OA:OD=OB:OC=n,则x=$\frac{a-bn}{2}$.(用a,b,n表示).
分析 利用对顶角相等得到∠AOB=∠COD,加上OA:OD=OB:OC=n,则可判断△OAB∽△ODC,于是可利用相似比得AB=nCD,由于AB=a-2x,则a-2x=bn,然后解关于x的方程即可.
解答 解:∵∠AOB=∠COD,
而OA:OD=OB:OC=n,
∴△OAB∽△ODC,
∴$\frac{AB}{CD}$=$\frac{OA}{OD}$=n,
∵AB=a-2x,
∴a-2x=bn,
∴x=$\frac{a-bn}{2}$.
故答案为$\frac{a-bn}{2}$.
点评 本题考查了相似三角形的应用:通常利用相似三角形的性质即相似三角形的对应边的比相等计算对应线段的长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.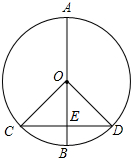 如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论错误的是( )
如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论错误的是( )
 如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论错误的是( )
如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论错误的是( )| A. | ∠AOC=∠AOD | B. | BE=OE | C. | CE=DE | D. | AC=AD |
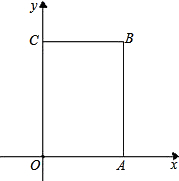 如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动.
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动.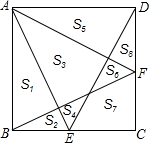 如图,正方形ABCD中,E,F分别是BC,CD边上的点,AE,DE,BF,AF把正方形分成8小块,试比较S3与S2+S7+S8的大小,并说明理由.
如图,正方形ABCD中,E,F分别是BC,CD边上的点,AE,DE,BF,AF把正方形分成8小块,试比较S3与S2+S7+S8的大小,并说明理由.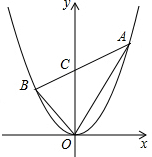 如图,过点C(0,3)的直线交抛物线y=x2于A、B两点,若S△AOB=6,求点A、B的坐标.
如图,过点C(0,3)的直线交抛物线y=x2于A、B两点,若S△AOB=6,求点A、B的坐标. 小刚要从A地赶往C地去参加科技夏令营,他拿出一张地图,图上有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A的南偏西55°,在B地的北偏西70°,如图所示.
小刚要从A地赶往C地去参加科技夏令营,他拿出一张地图,图上有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A的南偏西55°,在B地的北偏西70°,如图所示.