题目内容
9.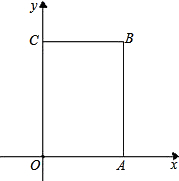 如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动.
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动.(1)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
(2)在移动过程中,当△OBP的面积是10时,求点P移动的时间.
分析 (1)先求得点P运动的距离,从而可得到点P的坐标;
(2)分为点P在OC、BC、AB、AO上分类计算即可.
解答 解:(1)2×4=8,
∴点P的坐标为(2,6).
(2)如图1所示: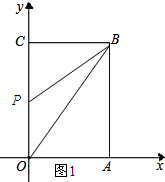
∵△OBP的面积=10,
∴$\frac{1}{2}OP•BC=10$,即$\frac{1}{2}×4×OP$=10.
解得:OP=5.
∴点P的坐标为(0,5).
如图2所示;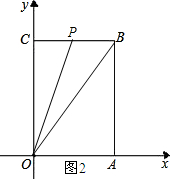
∵△OBP的面积=10,
∴$\frac{1}{2}PB•OC=10$,即$\frac{1}{2}×6×PB$=10.
解得:BP=$\frac{10}{3}$.
∴CP=$\frac{2}{3}$.
∴点P的坐标为($\frac{2}{3}$,6).
如图3所示: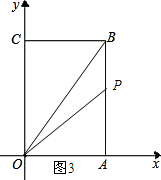
∵△OBP的面积=10,
∴$\frac{1}{2}BP•BC$=10,即$\frac{1}{2}×4×PB=10$.
解得:BP=5.
∴点P的坐标为(4,1).
如图4所示: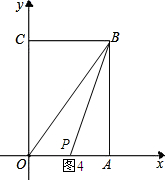
∵△OBP的面积=10,
∴$\frac{1}{2}OP•AB$=10,即$\frac{1}{2}×6×OP$=10.
解得:OP=$\frac{10}{3}$.
∴点P的坐标为($\frac{10}{3}$,0).
综上所述,点P的坐标为(0,5)或($\frac{10}{3}$,0)或(4,1)或($\frac{2}{3}$,6).
点评 本题主要考查的是三角形的面积公式的应用,分类讨论是解题的关键.

练习册系列答案
相关题目
12.下列说法错误的是( )
| A. | 由一个平面图形得到它的轴对称图形叫作轴对称变换 | |
| B. | 将一个图形沿一条直线折叠叫作轴对称变换 | |
| C. | 对称轴方向和位置发生变化时,得到的图形方向和位置也发生变化 | |
| D. | 成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到 |
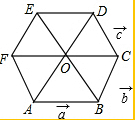 如图,在正六边形ABCDEF(由六个完全相同的等边三角形拼成)中,已知$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$.
如图,在正六边形ABCDEF(由六个完全相同的等边三角形拼成)中,已知$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$.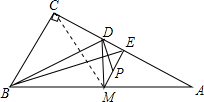 如图,Rt△ABC中,∠C=90°,点D在AC上,BD=AD,M是AB的中点,AE⊥AC于E,点P是ME的中点,连接DP,求证:BE⊥DP.
如图,Rt△ABC中,∠C=90°,点D在AC上,BD=AD,M是AB的中点,AE⊥AC于E,点P是ME的中点,连接DP,求证:BE⊥DP.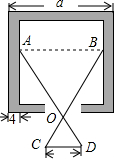 如图,若OA:OD=OB:OC=n,则x=$\frac{a-bn}{2}$.(用a,b,n表示).
如图,若OA:OD=OB:OC=n,则x=$\frac{a-bn}{2}$.(用a,b,n表示).