题目内容
20.已知直角坐标系中有A(-2,0),B(0,2),点P是y轴上的一点,若△ABP是等腰三角形,则点P的坐标是(0,2-2$\sqrt{2}$),(0,2+2$\sqrt{2}$),(0,-2),(0,0).分析 首先根据题意画出图形,然后分别从BP=AB,AP=AB,AP=BP去分析求解即可求得答案.
解答  解:如图,∵A(-2,0),B(0,2),
解:如图,∵A(-2,0),B(0,2),
∴OA=2,OB=2,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2$\sqrt{2}$;
①若BP=AB=2$\sqrt{2}$,则OP1=BP-OB=2$\sqrt{2}$-2,OP2=BP+OB=2$\sqrt{2}$+1,
∴点P1(0,2-2$\sqrt{2}$),点P2(0,2+2$\sqrt{2}$);
②若AP=AB,则OP3=OB=2,
∴点P3(0,-2);
③若AP=BP,则P4与O重合,
∴点P4(0,0);
综上所述:点P的坐标是:(0,2-2$\sqrt{2}$),(0,2+2$\sqrt{2}$),(0,-2),(0,0).
故答案为:(0,2-2$\sqrt{2}$),(0,2+2$\sqrt{2}$),(0,-2),(0,0).
点评 此题考查了等腰三角形的性质.注意首先求得AB的长,然后利用分类讨论思想求解是关键.

练习册系列答案
相关题目
12.下列说法错误的是( )
| A. | 由一个平面图形得到它的轴对称图形叫作轴对称变换 | |
| B. | 将一个图形沿一条直线折叠叫作轴对称变换 | |
| C. | 对称轴方向和位置发生变化时,得到的图形方向和位置也发生变化 | |
| D. | 成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到 |

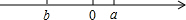 已知数a,b在数轴上对应点的位置如图所示,则下列结论正确的是②③④⑤⑥(填序号).
已知数a,b在数轴上对应点的位置如图所示,则下列结论正确的是②③④⑤⑥(填序号).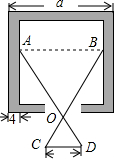 如图,若OA:OD=OB:OC=n,则x=$\frac{a-bn}{2}$.(用a,b,n表示).
如图,若OA:OD=OB:OC=n,则x=$\frac{a-bn}{2}$.(用a,b,n表示).