题目内容
13.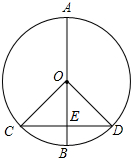 如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论错误的是( )
如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论错误的是( )| A. | ∠AOC=∠AOD | B. | BE=OE | C. | CE=DE | D. | AC=AD |
分析 根据等腰三角形性质求出∠COB=∠DOB,根据邻补角即可求出∠AOC=∠AOD,根据垂径定理即可求出CE=DE,根据线段垂直平分线即可求出AC=AD.
解答 解:A、∵AB⊥CD,OC=OD,
∴∠COB=∠DOB,
∴∠AOC+∠COB=180°,∠AOD+∠DOB=180°,
∴∠AOC=∠AOD,故本选项错误;
B、根据已知不能推出BE=OE,故本选项正确;
C、∵AB⊥CD,AB为直径,
∴CE=DE,故本选项错误;
D、∵AB⊥CD,AB过O,
∴CE=DE,
∴AC=AD,故本选项错误;
故选B.
点评 本题考查了等腰三角形的性质,垂径定理,线段垂直平分线性质的应用,能熟记定理的内容是解此题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
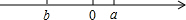 已知数a,b在数轴上对应点的位置如图所示,则下列结论正确的是②③④⑤⑥(填序号).
已知数a,b在数轴上对应点的位置如图所示,则下列结论正确的是②③④⑤⑥(填序号).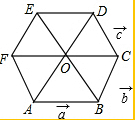 如图,在正六边形ABCDEF(由六个完全相同的等边三角形拼成)中,已知$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$.
如图,在正六边形ABCDEF(由六个完全相同的等边三角形拼成)中,已知$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$.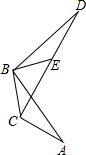 △ABC绕点B逆时针旋转90°得到△DBE,若恰好得到C,E,D三点共线,则AC、BC、CD的数量关系是$\sqrt{2}$BC+AC=CD.
△ABC绕点B逆时针旋转90°得到△DBE,若恰好得到C,E,D三点共线,则AC、BC、CD的数量关系是$\sqrt{2}$BC+AC=CD.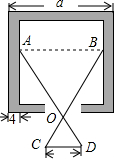 如图,若OA:OD=OB:OC=n,则x=$\frac{a-bn}{2}$.(用a,b,n表示).
如图,若OA:OD=OB:OC=n,则x=$\frac{a-bn}{2}$.(用a,b,n表示). 如图,在Rt△ABC中,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE是3cm,求BC.
如图,在Rt△ABC中,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE是3cm,求BC.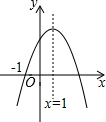 一次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①c<0;②b2-4ac>0;③a+2b=0;④当x>3,y>0.正确的个数是( )
一次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①c<0;②b2-4ac>0;③a+2b=0;④当x>3,y>0.正确的个数是( )