题目内容
17.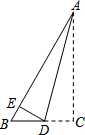 如图,直角三角形纸片ABC中,∠C=90°,∠BAC=30°,BC=1,将其沿AD折叠,使点C落在AB上的点E处.
如图,直角三角形纸片ABC中,∠C=90°,∠BAC=30°,BC=1,将其沿AD折叠,使点C落在AB上的点E处.(1)求AB与AC的长;
(2)求tan15°的值.
分析 (1)运用直角三角形的边角关系、勾股定理,求出AB、AC的长,即可解决问题.
(2)运用翻折变换的性质,证明DE=DC(设为λ),得到BD=1-λ;运用勾股定理列出关于λ的方程,求出λ,即可解决问题.
解答  解:(1)如图,∵∠C=90°,∠BAC=30°,BC=1,
解:(1)如图,∵∠C=90°,∠BAC=30°,BC=1,
∴AB=2;由勾股定理得:AC=$\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$.
(2)由题意得:
DE=DC(设为λ),∠EAD=∠CAD=15°,
AE=AC=$\sqrt{3}$,∠AED=∠C=90°,
则BD=1-λ,BE=2-$\sqrt{3}$,∠BED=90°,
由勾股定理得:$(1-λ)^{2}=(2-\sqrt{3})^{2}+{λ}^{2}$,
解得:λ=2$\sqrt{3}$-3,
故tan15°=$\frac{DC}{AC}$=$\frac{2\sqrt{3}-3}{\sqrt{3}}$=2-$\sqrt{3}$.
点评 该题主要考查了翻折变换的性质、勾股定理、正切函数的定义等知识点及其应用问题;应牢固掌握翻折变换的性质等几何知识点,这是灵活运用、解题的基础和关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.平面直角坐标系中,已知A(6,0),△AOP为等腰三角形且面积为12,满足条件的P点有( )
| A. | 4个 | B. | 8个 | C. | 10个 | D. | 12个 |
6.运算结果是1-2ab2+a2b4的是( )
| A. | (-1+ab2)2 | B. | (1+a2b2)2 | C. | (-1+a2b2)2 | D. | (-1-a2b2)2 |
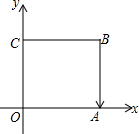 如图,长方形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(4,0)、(0,5),点B在第一象限内.
如图,长方形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(4,0)、(0,5),点B在第一象限内.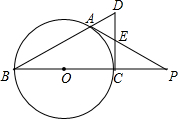 如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.
如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.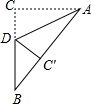 如图,在△ABC中,∠ACB=90°,AC=3,BC=4,D是BC上一点,若沿AD折叠,则点C落在AB上的点C处,求S△ABD.
如图,在△ABC中,∠ACB=90°,AC=3,BC=4,D是BC上一点,若沿AD折叠,则点C落在AB上的点C处,求S△ABD.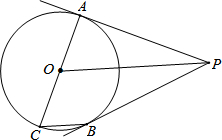 如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,点B为⊙O上一点,满足BC∥OP.
如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,点B为⊙O上一点,满足BC∥OP.