题目内容
2.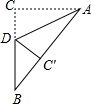 如图,在△ABC中,∠ACB=90°,AC=3,BC=4,D是BC上一点,若沿AD折叠,则点C落在AB上的点C处,求S△ABD.
如图,在△ABC中,∠ACB=90°,AC=3,BC=4,D是BC上一点,若沿AD折叠,则点C落在AB上的点C处,求S△ABD.
分析 如图,首先求出AB=5;其次证明AC′=AC=3,CD=C′D(设为λ);在直角△BDC′中,运用勾股定理列出关于λ的方程,求出λ;运用三角形的面积公式即可解决问题.
解答  解:如图,∵∠ACB=90°,AC=3,BC=4,
解:如图,∵∠ACB=90°,AC=3,BC=4,
∴由勾股定理得:AB=5;
由题意得:AC′=AC=3,CD=C′D(设为λ),
∠AC′D=∠ACD=90°,
∴∠DC′B=90°,BC′=2,BD=4-λ;
由勾股定理得:(4-λ)2=λ2+22,
解得:λ=$\frac{3}{2}$,BD=$\frac{5}{2}$,
∴${S}_{△ABD}=\frac{1}{2}×\frac{5}{2}×3$=$\frac{15}{4}$.
点评 该题主要考查了翻折变换的性质、勾股定理、三角形的面积公式等几何知识点及其应用问题;观察图形,准确找出图形中隐含的等量关系是基础,灵活运用翻折变换的性质等知识点来解题是关键.

练习册系列答案
相关题目
13.同一副三角板(两块)画角,不可能画出的角的度数是( )
| A. | 135° | B. | 75° | C. | 55° | D. | 15° |
7.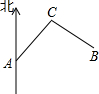 如图,我国鱼政救助船在海上自南向北航行,同时,一艘鱼船从B港出发沿北偏西60°方向航行,t小时后,鱼政救助船到达A处,鱼船到达C处,此时鱼政救助船测得该鱼船在北偏东40°方向,则此时鱼船观测港口与鱼政救助船的视角∠ACB为( )
如图,我国鱼政救助船在海上自南向北航行,同时,一艘鱼船从B港出发沿北偏西60°方向航行,t小时后,鱼政救助船到达A处,鱼船到达C处,此时鱼政救助船测得该鱼船在北偏东40°方向,则此时鱼船观测港口与鱼政救助船的视角∠ACB为( )
 如图,我国鱼政救助船在海上自南向北航行,同时,一艘鱼船从B港出发沿北偏西60°方向航行,t小时后,鱼政救助船到达A处,鱼船到达C处,此时鱼政救助船测得该鱼船在北偏东40°方向,则此时鱼船观测港口与鱼政救助船的视角∠ACB为( )
如图,我国鱼政救助船在海上自南向北航行,同时,一艘鱼船从B港出发沿北偏西60°方向航行,t小时后,鱼政救助船到达A处,鱼船到达C处,此时鱼政救助船测得该鱼船在北偏东40°方向,则此时鱼船观测港口与鱼政救助船的视角∠ACB为( )| A. | 60° | B. | 80° | C. | 90° | D. | 100° |
14.在△ABC中,∠C=90°,AB=12,BC=5,则AC的长为( )
| A. | 12 | B. | 13 | C. | $\sqrt{119}$ | D. | 15 |
11.a=-0.32,b=-3-2,c=(-3)-2,d=(-$\frac{1}{3}$)0,则( )
| A. | a<b<d<c | B. | a<d<c<b | C. | b<a<c<d | D. | c<a<d<b |
12.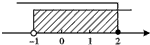 如图,下列哪个不等式组的解集在数轴上表示如图所示( )
如图,下列哪个不等式组的解集在数轴上表示如图所示( )
 如图,下列哪个不等式组的解集在数轴上表示如图所示( )
如图,下列哪个不等式组的解集在数轴上表示如图所示( )| A. | $\left\{\begin{array}{l}{x≤2}\\{x>-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≥2}\\{x<-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x>2}\\{x≤-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x<2}\\{x≥-1}\end{array}\right.$ |
 如图,已知△ABC中,∠A=60°,D为AB上一点,且AC=2AD+BD,∠B=4∠ACD,则∠DCB的度数是20°.
如图,已知△ABC中,∠A=60°,D为AB上一点,且AC=2AD+BD,∠B=4∠ACD,则∠DCB的度数是20°.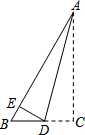 如图,直角三角形纸片ABC中,∠C=90°,∠BAC=30°,BC=1,将其沿AD折叠,使点C落在AB上的点E处.
如图,直角三角形纸片ABC中,∠C=90°,∠BAC=30°,BC=1,将其沿AD折叠,使点C落在AB上的点E处.