题目内容
7.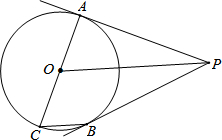 如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,点B为⊙O上一点,满足BC∥OP.
如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,点B为⊙O上一点,满足BC∥OP.(1)求证:PB是⊙O的切线;
(2)若cos∠ACB=$\frac{3}{5}$,求sin∠APB的值.
分析 (1)连接OB,证明△AOP≌△BOP,得出对应角相等,∠OBP=∠OAP=90°,即可得出结论;
(2)连接AB交OP于点M,过A作AB⊥BP于点Q,先求出cos∠BAP=$\frac{AM}{AP}$=$\frac{3}{5}$,令AM=3,AP=5,得出PM=4,AB=5,BP=6,根据面积求出AQ,再由锐角三角函数的定义即可得出结果.
解答 (1)证明:连接OB;如图所示: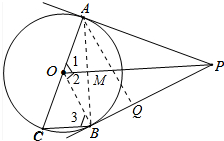
∵PA是⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
∵OP∥BC,
∴∠1=∠C,∠2=∠3,
∵OC=OB,
∴∠C=∠3,
∴∠1=∠2,
在△AOP和△BOP中,
$\left\{\begin{array}{l}{AO=BO}&{\;}\\{∠1=∠2}&{\;}\\{OP=OP}&{\;}\end{array}\right.$,
∴△AOP≌△BOP(SAS),
∴∠OBP=∠OAP=90°,
∴OB⊥BP,且OB为半径,
∴PB是⊙O的切线;
(2)连接AB交OP于点M,过A作AQ⊥BP于点Q;如图所示:
∵AP、BP为⊙O的切线,
∴PA=PB,
∵AO=BO,
∴OP垂直平分AB,
∵AC为直径,
∴∠ABC=90°,
∴∠C+∠CAB=90°,
∵∠CAB+∠BAP=90°,
∴∠C=∠BAP,
∴cos∠BAP=cos∠ACB=$\frac{3}{5}$,
∵AB⊥OP,
∴∠AMP=90°,
∴cos∠BAP=$\frac{AM}{AP}$=$\frac{3}{5}$,
令AM=3,AP=5,
∴PM=4,AB=5,BP=6,
∴S△ABP=$\frac{1}{2}$AQ•BP=$\frac{1}{2}$AB•PM,
∴AQ=$\frac{AB•PM}{BP}$=$\frac{24}{5}$,
∵AQ⊥BP,
∴∠AQP=90°,
∴sin∠APB=$\frac{AQ}{AP}$=$\frac{\frac{24}{5}}{5}$=$\frac{24}{25}$.
点评 本题考查了切线的判定与性质、全等三角形的判定与性质、锐角三角函数的定义、三角形面积的计算方法;熟练掌握切线的判定与性质进行有关计算是解决问题的关键.

①如果一个事件发生的可能性很小,那么他就不可能发生
②如果一个事件发生的概率很大,那么他就必然发生
③如果一个事件不可能发生,那么其发生的概率为0.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
| A. | a3-a=a2 | B. | (-2a)2=4a2 | C. | x3•x-2=x-6 | D. | x6÷x3=x2 |
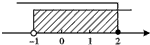 如图,下列哪个不等式组的解集在数轴上表示如图所示( )
如图,下列哪个不等式组的解集在数轴上表示如图所示( )| A. | $\left\{\begin{array}{l}{x≤2}\\{x>-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≥2}\\{x<-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x>2}\\{x≤-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x<2}\\{x≥-1}\end{array}\right.$ |
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
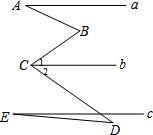 如图,a∥b∥c,∠A=25°,∠1=35°,∠2=45°,∠E=15°,则∠ABC与∠CDE的度数分别为( )
如图,a∥b∥c,∠A=25°,∠1=35°,∠2=45°,∠E=15°,则∠ABC与∠CDE的度数分别为( )| A. | 50°,30° | B. | 60°,30° | C. | 50°,20° | D. | 60°,20° |
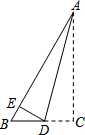 如图,直角三角形纸片ABC中,∠C=90°,∠BAC=30°,BC=1,将其沿AD折叠,使点C落在AB上的点E处.
如图,直角三角形纸片ABC中,∠C=90°,∠BAC=30°,BC=1,将其沿AD折叠,使点C落在AB上的点E处.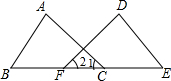 在数学实践课上,老师在黑板上画出如图的图形,(其中点B,F,C,E在同一条直线上).并写出四个条件:①AB=DE,②∠1=∠2.③BF=EC,④∠B=∠E,交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.
在数学实践课上,老师在黑板上画出如图的图形,(其中点B,F,C,E在同一条直线上).并写出四个条件:①AB=DE,②∠1=∠2.③BF=EC,④∠B=∠E,交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.