题目内容
9.平面直角坐标系中,已知A(6,0),△AOP为等腰三角形且面积为12,满足条件的P点有( )| A. | 4个 | B. | 8个 | C. | 10个 | D. | 12个 |
分析 先利用△AOP的面积为12,求得边OA上的高,然后分三种情况考虑:①当AO=AP时,②当OA=OP时,③当OP=AP时,分别求得点P的个数,即可得出答案.
解答 解:∵A(6,0),
∴OA=6,
设△AOP的边OA上的高是h,
则$\frac{1}{2}$×6×h=12,
解得:h=4,
在x轴的两侧作直线a和直线b都和x轴平行,且到x轴的距离都等于4,如图:
①当AO=AP时,以点A为圆心,以6为半径画弧,交直线a和直线b分别有两个点,即共4个点符合,
②当OA=OP时,以O为圆心,以6为半径画弧,交直线a和直线b分别有两个点,即共4个点符合,
③当OP=AP时,作AO的垂直平分线分别交直线a、b于一点,即共2个点符合,
4+4+2=10.
故选:C.
点评 本题主要考查了坐标与图形的性质及等腰三角形的判定;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.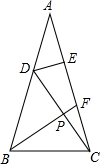 如图△ABC中,∠A=36°,AB=AC,BF平分∠ABC,E是AF的中点,DE⊥AC交AB于D,连接DC交BF于P,∠DPB的度数是( )
如图△ABC中,∠A=36°,AB=AC,BF平分∠ABC,E是AF的中点,DE⊥AC交AB于D,连接DC交BF于P,∠DPB的度数是( )
 如图△ABC中,∠A=36°,AB=AC,BF平分∠ABC,E是AF的中点,DE⊥AC交AB于D,连接DC交BF于P,∠DPB的度数是( )
如图△ABC中,∠A=36°,AB=AC,BF平分∠ABC,E是AF的中点,DE⊥AC交AB于D,连接DC交BF于P,∠DPB的度数是( )| A. | 36° | B. | 54° | C. | 72° | D. | 90° |
14.在△ABC中,∠C=90°,AB=12,BC=5,则AC的长为( )
| A. | 12 | B. | 13 | C. | $\sqrt{119}$ | D. | 15 |
1.据调查,2011年5月张掖市的房价均价为3600元/m2,2013年同期将达到4200元/m2,假设这两年张掖市房价的平均增长率为x,根据题意,所列方程为( )
| A. | 3600(1+x%)2=4200 | B. | 3600(1-x%)2=4200 | C. | 3600(1+x)2=4200 | D. | 3600(1-x)2=4200 |
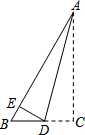 如图,直角三角形纸片ABC中,∠C=90°,∠BAC=30°,BC=1,将其沿AD折叠,使点C落在AB上的点E处.
如图,直角三角形纸片ABC中,∠C=90°,∠BAC=30°,BC=1,将其沿AD折叠,使点C落在AB上的点E处.