Question

15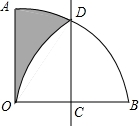．如图，扇形AOB的圆心角为90°，半径为2，点C为OB中点，点D在$\widehat{AB}$上，将扇形沿直线CD折叠，若点B，O重合，则图中阴影部分的周长为π+2．（结果保留π）

Answer 1

分析 根据折叠的性质得到$\widehat{OD}$=$\widehat{BD}$，利用扇形的弧长的计算$\widehat{AB}$的长，根据周长公式计算即可．

解答 解：$\widehat{AB}$的长为$\frac{90π×2}{180}$=π，
由折叠的性质可知，$\widehat{OD}$=$\widehat{BD}$，
∴图中阴影部分的周长=AO+$\widehat{AD}$+$\widehat{OD}$=AO+$\widehat{AB}$=π+2，
故答案为：π+2．

点评 本题考查的是扇形的弧长的计算和折叠的性质，掌握弧长公式、理解折叠前后两个图形能够重合是解题的关键．