题目内容
12.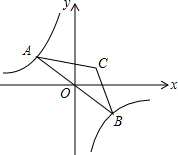 如图,点A是双曲线y=-$\frac{9}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为3.
如图,点A是双曲线y=-$\frac{9}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为3.
分析 连接CO,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,证明△AOD∽△OCE,根据相似三角形的性质求出△AOD和△OCE面积比,根据反比例函数图象上点的特征求出S△AOD,得到S△EOC,求出k的值.
解答 解:连接CO,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,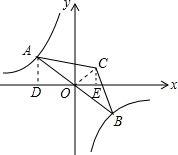
∵连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,
∴CO⊥AB,∠CAB=30°,
则∠AOD+∠COE=90°,
∵∠DAO+∠AOD=90°,
∴∠DAO=∠COE,
又∵∠ADO=∠CEO=90°,
∴△AOD∽△OCE,
∴$\frac{AD}{EO}$=$\frac{OD}{CE}$=$\frac{OA}{OC}$=tan60°=$\sqrt{3}$,
∴$\frac{{S}_{△AOD}}{{S}_{△EOC}}$=($\sqrt{3}$)2=3,
∵点A是双曲线y=-$\frac{9}{x}$在第二象限分支上的一个动点,
∴S△AOD=$\frac{1}{2}$×|xy|=$\frac{9}{2}$,
∴S△EOC=$\frac{3}{2}$,即$\frac{1}{2}$×OE×CE=$\frac{3}{2}$,
∴k=OE×CE=3,
故答案为:3.
点评 此题主要考查了反比例函数与一次函数的交点以及相似三角形的判定与性质,得出△AOD∽△OCE是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知点(x1,y1)、(x2,y2)、(x3,y3)在双曲线$y=\frac{5}{x}$上,当x1<0<x2<x3时,y1、y2、y3的大小关系是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y2<y3<y1 |
7.我国“天河二号”计算机的运算速度世界最快,若完成一次基本运算的时间约为0.000 000 000 001s,把这个数用科学记数法可表示为( )
| A. | 0.1×10-11s | B. | 0.1×10-12s | C. | 1×10-11s | D. | 1×10-12s |
17.已知a,b是一元二次方程x2-2x-1=0的两个实数根,则代数式(a-b)(a+b-2)+ab的值等于( )
| A. | -1 | B. | 1 | C. | ±8$\sqrt{2}$-1 | D. | ±8$\sqrt{2}$+1 |
 Rt△ABC中,∠B=90°,∠BAC=78°,过C作CF∥AB,连接AF与BC相交于G,若GF=2AC,求∠BAG的大小.
Rt△ABC中,∠B=90°,∠BAC=78°,过C作CF∥AB,连接AF与BC相交于G,若GF=2AC,求∠BAG的大小.
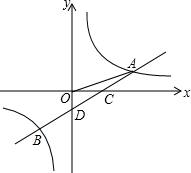 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知A(3,1),点B的坐标为(m,-2).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知A(3,1),点B的坐标为(m,-2).