题目内容
12．
如图，AB∥CD，AD⊥BD，∠1=55°，则∠2的大小是35°．
分析 由AB∥CD，∠1=55°，根据两直线平行，同旁内角互补，可求得∠BDC的度数，又由AD⊥BD，即可求得答案．
解答 解：∵AB∥CD，∠1=55°，
∴∠BDC=180°-∠1=125°，
∵AD⊥BD，
∴∠ADB=90°，
∴∠2=∠BDC-∠ADB=35°．
故答案为：35°．
点评 此题考查了平行线的性质以及垂线的定义．注意掌握两直线平行，同旁内角互补定理的应用是解此题的关键．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
2．甲乙两家商场平时以同样的价格出售相同的商品．春节期间两家商场都让利酬宾，其中甲商场所有商品按8折出售，乙商场对一次购物中超过200元后的价格部分打7折．
设x（单位：元）表示商品原价，y（单位：元）表示购物金额．
（Ⅰ）根据题意，填写下表：（单位：元）
（Ⅱ）分别就两家商场的让利方式，写出y关于x的函数解析式；
（Ⅲ）春节期间，当在同一商场累计购物超过200元时，哪家商场的实际花费少？
设x（单位：元）表示商品原价，y（单位：元）表示购物金额．
（Ⅰ）根据题意，填写下表：（单位：元）
| 商品价格 购物金额 | 120 | 180 | 200 | 260 |
| 甲商场 | 96 | 144 | 160 | 208 |
| 乙商场 | 120 | 180 | 200 | 242 |
（Ⅲ）春节期间，当在同一商场累计购物超过200元时，哪家商场的实际花费少？
3．一个观察员要到如图1所示的A，B，C，D四个观测点进行观测，行进路线由在同一平面上的AB，BC，CD，DA，AC，BD组成．为记录观察员的行进路线，在AB的中点M处放置了一台定位仪器，设观察员行进的路程为x，观察员与定位仪器之间的距离为y，若观察员匀速行进，且表示y与x的函数关系的图象大致如图2所示，则观察员的行进路线可能为（ ）
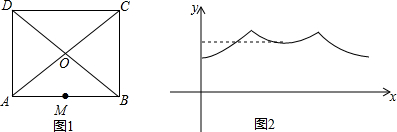
| A． | A→D→C→B | B． | A→B→C→D | C． | A→C→B→D | D． | A→C→D→B |
20．一蓄水池有水40m3，如果每分钟放出2m3的水，水池里的水量y（m3）与放水时间t（分）有如下关系：
下列结论中正确的是（ ）
| 放水时间（分） | 1 | 2 | 3 | 4 | … |
| 水池中水量（m3） | 38 | 36 | 34 | 32 | … |
| A． | y随t的增加而增大 | |
| B． | 放水时为20分钟时，水池中水量为8m3 | |
| C． | y与t之间的关系式为y=40-t | |
| D． | 放水时为18分钟时，水池中水量为4m3 |
7．
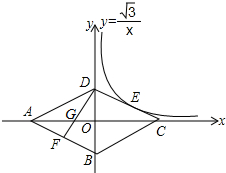如图，菱形ABCD的四个顶点均在坐标轴上，对角线AC、BD交于原点O，DF⊥AB交AC于点G，反比例函数y=$\frac{\sqrt{3}}{x}$（x＞0）经过线段DC的中点E，若BD=4，则AG的长为（ ）
如图，菱形ABCD的四个顶点均在坐标轴上，对角线AC、BD交于原点O，DF⊥AB交AC于点G，反比例函数y=$\frac{\sqrt{3}}{x}$（x＞0）经过线段DC的中点E，若BD=4，则AG的长为（ ）| A． | $\frac{4\sqrt{3}}{3}$ | B． | $\sqrt{3}$+2 | C． | 2$\sqrt{3}$+1 | D． | $\frac{3\sqrt{3}}{2}$+1 |
4．当0≤x≤3时，一次函数y=-x+3的最大值是（ ）
| A． | 0 | B． | 3 | C． | -3 | D． | 无法确定 |
1．计算3x2•（-2x）3的结果是（ ）
| A． | -18x5 | B． | -24x5 | C． | -24x6 | D． | -18x6 |
2．已知二次函数y=x2-2mx+m2+3（m为常数），下列结论正确的是（ ）
| A． | 当m=0时，二次函数图象的顶点坐标为（0，0） | |
| B． | 当m＜0时，二次函数图象的对称轴在y轴右侧 | |
| C． | 若将该函数图象沿y轴向下平移6个单位，则平移后图象与x轴两交点之间的距离为$2\sqrt{3}$ | |
| D． | 设二次函数的图象与y轴交点为A，过A作x轴的平行线，交图象于另一点B，抛物线的顶点为C，则△ABC的面积为m3 |