题目内容
3.(1)$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$(2)(4$\sqrt{12}$+$\frac{1}{4}$$\sqrt{48}$-9$\sqrt{\frac{1}{3}}$)÷$\sqrt{18}$.
分析 (1)先利用二次根式的乘除法则运算,然后化简后合并即可;
(2)先把二次根式化为最简二次根式,然后把括号内合并后进行二次根式的除法运算.
解答 解:(1)原式=$\sqrt{48÷3}$-$\sqrt{\frac{1}{2}×12}$+2$\sqrt{6}$
=4-$\sqrt{6}$+2$\sqrt{6}$
=4+$\sqrt{6}$;
(2)原式=(8$\sqrt{3}$+$\sqrt{3}$-3$\sqrt{3}$)÷3$\sqrt{2}$
=6$\sqrt{3}$÷3$\sqrt{2}$
=$\sqrt{6}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
14. 如图,∠BAC=80°,BO、CO分别平分∠ABC和∠ACB,则∠BOC=( )
如图,∠BAC=80°,BO、CO分别平分∠ABC和∠ACB,则∠BOC=( )
 如图,∠BAC=80°,BO、CO分别平分∠ABC和∠ACB,则∠BOC=( )
如图,∠BAC=80°,BO、CO分别平分∠ABC和∠ACB,则∠BOC=( )| A. | 100° | B. | 130° | C. | 140° | D. | 150° |
11.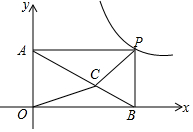 如图,P是双曲线y=$\frac{6}{x}$(x>0)上任意一点,作PB⊥x轴于B,PA⊥y轴于A,C是平行四边形OAPB内任意一点,连接CA、CO、CB、CP,则△OCB与△ACP的面积和等于( )
如图,P是双曲线y=$\frac{6}{x}$(x>0)上任意一点,作PB⊥x轴于B,PA⊥y轴于A,C是平行四边形OAPB内任意一点,连接CA、CO、CB、CP,则△OCB与△ACP的面积和等于( )
 如图,P是双曲线y=$\frac{6}{x}$(x>0)上任意一点,作PB⊥x轴于B,PA⊥y轴于A,C是平行四边形OAPB内任意一点,连接CA、CO、CB、CP,则△OCB与△ACP的面积和等于( )
如图,P是双曲线y=$\frac{6}{x}$(x>0)上任意一点,作PB⊥x轴于B,PA⊥y轴于A,C是平行四边形OAPB内任意一点,连接CA、CO、CB、CP,则△OCB与△ACP的面积和等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.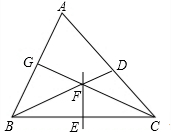 如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )
如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )
 如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )
如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
13.下列判断:
①对角线相等的四边形是矩形
②对角线互相垂直的四边形是菱形
③对角线互相垂直的矩形是正方形
其中,正确的有( )
①对角线相等的四边形是矩形
②对角线互相垂直的四边形是菱形
③对角线互相垂直的矩形是正方形
其中,正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
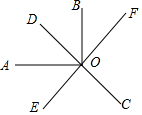 如图,已知直线CD、EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=30°.
如图,已知直线CD、EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=30°.