题目内容
18.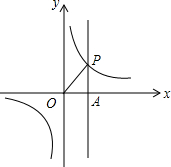 如图,函数y=$\frac{k}{x}$的图象与直线x=2交于第一象限的点P,△AOP的面积等于$\frac{1}{2}$.
如图,函数y=$\frac{k}{x}$的图象与直线x=2交于第一象限的点P,△AOP的面积等于$\frac{1}{2}$.(1)利用图象,求当0<x<2时,y的取值范围;
(2)设P1(x1,y1),P2(x2,y2)是函数y=$\frac{k}{x}$图象上的任意不重合的两点,M=$\frac{{y}_{1}}{{x}_{1}}$+$\frac{{y}_{2}}{{x}_{2}}$,N=$\frac{{y}_{2}}{{x}_{1}}$+$\frac{{y}_{1}}{{x}_{2}}$试判断M,N的大小.并说明理由.
分析 (1)根据条件易求出点P的坐标,然后只需结合图象就可解决问题;
(2)根据点P的坐标可求出反比例函数的解析式,从而得到y1与x1、y2与x2的关系,然后只需运用作差法就可解决问题.
解答 解:(1)由题意可得OA=2,S△AOP=$\frac{1}{2}$,
则$\frac{1}{2}$×2×AP=$\frac{1}{2}$,
解得AP=$\frac{1}{2}$,
∴点P的坐标为(2,$\frac{1}{2}$).
结合图象可得:
当0<x<2时,y的取值范围是y>$\frac{1}{2}$;
(2)M>N.
理由如下:∵点P(2,$\frac{1}{2}$)在函数y=$\frac{k}{x}$的图象上,
∴k=2×$\frac{1}{2}$=1,y=$\frac{1}{x}$.
∵P1(x1,y1),P2(x2,y2)是函数y=$\frac{1}{x}$图象上的任意不重合的两点,
∴y1=$\frac{1}{{x}_{1}}$,y2=$\frac{1}{{x}_{2}}$,y1≠y2.
∵M=$\frac{{y}_{1}}{{x}_{1}}$+$\frac{{y}_{2}}{{x}_{2}}$,N=$\frac{{y}_{2}}{{x}_{1}}$+$\frac{{y}_{1}}{{x}_{2}}$,
∴M-N=($\frac{{y}_{1}}{{x}_{1}}$+$\frac{{y}_{2}}{{x}_{2}}$)-($\frac{{y}_{2}}{{x}_{1}}$+$\frac{{y}_{1}}{{x}_{2}}$)
=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}}$+$\frac{{y}_{2}-{y}_{1}}{{x}_{2}}$
=(y1-y2)($\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$)
=(y1-y2)2>0,
∴M>N.
点评 本题主要考查了反比例函数图象上点的坐标特征,在解决问题的过程中用到了数形结合和作差法等重要的数学思想方法,应熟练掌握.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 得分/分 | 0 | 1 | 2 | 3 | 4 |
| 百分率 | 15% | 10% | 25% | 40% | 10% |
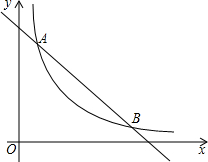 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$与一次函数y=-x+b交于点A(1,6-k),B(m,1).
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$与一次函数y=-x+b交于点A(1,6-k),B(m,1).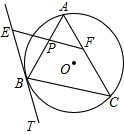 如图,△ABC是⊙O的内接三角形,BT是⊙O的切线,P是线段AB上一点,经过P作BC的平行线与BT交于E点,与AC交于F点.
如图,△ABC是⊙O的内接三角形,BT是⊙O的切线,P是线段AB上一点,经过P作BC的平行线与BT交于E点,与AC交于F点. 如图,点P是等腰Rt△ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设点D为BC中点,求证:△DEF是等腰直角三角形.
如图,点P是等腰Rt△ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设点D为BC中点,求证:△DEF是等腰直角三角形.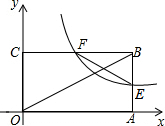 如图,矩形OABC中,OB=6,点O是坐标原点,点A,C分别在x轴,y轴的正半轴上,反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象分别交AB,BC于点E,F,F是BC的中点,则EF的长为3.
如图,矩形OABC中,OB=6,点O是坐标原点,点A,C分别在x轴,y轴的正半轴上,反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象分别交AB,BC于点E,F,F是BC的中点,则EF的长为3.