题目内容
12.已知⊙O的半径为13,弦AB∥CD,AB=24,CD=10,则AB、CD之间的距离为( )| A. | 17 | B. | 7 | C. | 12 | D. | 7或17 |
分析 分两种情况进行讨论:①弦AB和CD在圆心同侧;②弦AB和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可.
解答  解:①当弦AB和CD在圆心同侧时,如图1,
解:①当弦AB和CD在圆心同侧时,如图1,
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=12-5=7cm;
②当弦AB和CD在圆心异侧时,如图2,
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=OF+OE=17cm.
∴AB与CD之间的距离为7cm或17cm.
故选:D.
点评 本题考查了勾股定理和垂径定理的应用.此题难度适中,解题的关键是注意掌握数形结合思想与分类讨论思想的应用,小心别漏解.

练习册系列答案
相关题目
2.已知a,b,c是有理数,观察表中的运算,并在空格内填上相应的数.
| a,b,c的运算 | a+6b | 2a-5c | a-2b+7c | 2a+2b+c |
| 运算的结果 | -4 | 9 | -3 | 1 |
20.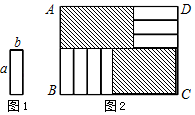 如图1,将7张长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
如图1,将7张长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
 如图1,将7张长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
如图1,将7张长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )| A. | a=b | B. | a=3b | C. | a=2b | D. | a=4b |
7.平面直角坐标系,第四象限内一点P到x轴的距离为2,到y轴的距离为5,那么点P坐标是( )
| A. | (2,-5) | B. | (-5,2) | C. | (-2,5) | D. | (5,-2) |
4. 如图,电路图上有四个开关A、B、C、D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是( )
如图,电路图上有四个开关A、B、C、D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是( )
 如图,电路图上有四个开关A、B、C、D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是( )
如图,电路图上有四个开关A、B、C、D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
2.下列运算正确的是( )
| A. | 2a•5b=10ab | B. | (2x2)3=2x5 | C. | 3+$\sqrt{2}$=3$\sqrt{2}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=2 |




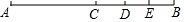 如图,已知线段AB=20,C是AB上的一点,D为CB上的一点,E为DB的中点,DE=3.
如图,已知线段AB=20,C是AB上的一点,D为CB上的一点,E为DB的中点,DE=3.