题目内容
7.平面直角坐标系,第四象限内一点P到x轴的距离为2,到y轴的距离为5,那么点P坐标是( )| A. | (2,-5) | B. | (-5,2) | C. | (-2,5) | D. | (5,-2) |
分析 根据第四象限内点的横坐标是正数,纵坐标是负数,点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.
解答 解:∵第四象限内一点P到x轴的距离为2,到y轴的距离为5,
∴点P的横坐标为5,纵坐标为-2,
∴点P坐标是(5,-2).
故选D.
点评 本题考查了点的坐标,主要利用了点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度.

练习册系列答案
相关题目
17.在学校,每一位同学都对应着一个学籍号.在数学中也有一些对应.现定义一种对应关系f,使得数对(x,y)和数z是对应的,此时把这种关系记作:f(x,y)=z.对于任意的数m,n(m>n),对应关系f由如表给出:
如:f(1,2)=2+1=3,f (2,1)=2-1=1,f (-1,-1)=-1,则使等式f(1+2x,3x)=2成立的x的值是-1.
| (x,y) | (n,n) | (m,n) | (n,m) |
| f(x,y) | n | m-n | m+n |
18. 如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=1,DB=2,则△ADE的面积与△ABC的面积的比等于( )
如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=1,DB=2,则△ADE的面积与△ABC的面积的比等于( )
 如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=1,DB=2,则△ADE的面积与△ABC的面积的比等于( )
如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=1,DB=2,则△ADE的面积与△ABC的面积的比等于( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{9}$ |
12.已知⊙O的半径为13,弦AB∥CD,AB=24,CD=10,则AB、CD之间的距离为( )
| A. | 17 | B. | 7 | C. | 12 | D. | 7或17 |
17.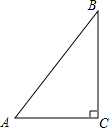 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{3}$ |
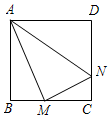 如图,正方形ABCD边长为8,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,始终保持AM和MN垂直,设BM=x,梯形ABCN的面积为y.
如图,正方形ABCD边长为8,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,始终保持AM和MN垂直,设BM=x,梯形ABCN的面积为y.