题目内容
3．在两个全等三角形中①如果两个三角形有公共边，那么沿公共边所在的直线折叠，能使这两个三角形重合
②如果两个三角形有公共顶点，那么以公共顶点为中心，把其中一个三角形绕中心旋转180°能与另一个三角形重合
③如果两个三角形有一对对应角是对顶角，则把其中一个三角形绕这对对应角的顶点旋转180°能与另一个三角形重合
以上说法正确的个数有（ ）
| A． | 3个 | B． | 2个 | C． | 1个 | D． | 0个 |
分析 ①注意全等三角形的对应角要相等；
②全等三角形的对应边要相等；
③全等三角形的对应边、对应角要相等．
解答 解：①若这两个全等三角形关于公共边对称时，沿公共边所在的直线折叠，能使这两个三角形重合，故错误；
②若这两个全等三角形关于公共顶点成中心对称时，以公共顶点为中心，把其中一个三角形绕中心旋转180°能与另一个三角形重合，故错误；
③若这两个全等三角形关于这一对对应角的顶点成中心对称时，把其中一个三角形绕这对对应角的顶点旋转180°能与另一个三角形重合，故错误；
故选：D．
点评 本题考查了几何变换的类型．对称有轴对称和中心对称，轴对称的特点是一个图形绕着一条直线对折，直线两旁的图形能够完全重合；中心对称的特点是一个图形绕着一点旋转180°后与另一个图形完全重合，它是旋转变换的一种特殊情况．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
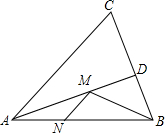如图，在锐角△ABC中，AB=6，∠BAC=60°，∠BAC的平分线交BC于点D，M、N是AD、AB上的动点，则BM+MN的最小值为3$\sqrt{3}$．
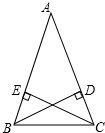如图，在△ABC中，AB=AC，CE，BD分别是AB，AC上的高．求证：BD=CE．
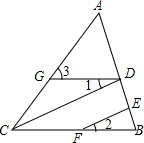填写推理理由：