题目内容
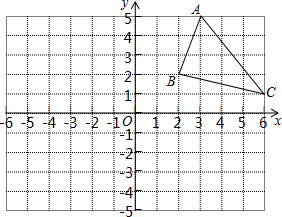 如图,△ABC的顶点坐标分别是A(2,2)、B(3,5)、C(6,1)
如图,△ABC的顶点坐标分别是A(2,2)、B(3,5)、C(6,1)(1)作△A′B′C′,使△ABC与△A′B′C′关于x轴对称;
(2)AB长度是
(3)△ABC
(4)△ABC的面积=
考点:作图-轴对称变换
专题:网格型
分析:(1)根据轴对称的性质画出△A′B′C′即可;
(2)由勾股定理可得出AB,BC的长;
(3)根据勾股定理的逆定理可判定出△ABC的形状;
(4)利用正方形的面积减去三角形三个顶点上三角形的面积即可.
(2)由勾股定理可得出AB,BC的长;
(3)根据勾股定理的逆定理可判定出△ABC的形状;
(4)利用正方形的面积减去三角形三个顶点上三角形的面积即可.
解答: 解:(1)如图所示;
解:(1)如图所示;
(2)AB=
=
,BC=
=
,
故答案为:无理数,
;
(3)∵AB2=12+32=10,BC2=12+42=17,AC2=32+42=25,10+17≠25,
∴△ABC不是直角三角形.
故答案为:不是;
(4)S△ABC=4×4-
×1×3-
×1×4-
×3×4=
.
故答案为:
.
 解:(1)如图所示;
解:(1)如图所示;(2)AB=
| 12+32 |
| 10 |
| 12+42 |
| 17 |
故答案为:无理数,
| 17 |
(3)∵AB2=12+32=10,BC2=12+42=17,AC2=32+42=25,10+17≠25,
∴△ABC不是直角三角形.
故答案为:不是;
(4)S△ABC=4×4-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 2 |
故答案为:
| 13 |
| 2 |
点评:本题考查的是作图-轴对称变换,熟知轴对称的性质是解答此题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
下列运算错误的是( )
| A、(-a)(-a)=(-a)2 |
| B、-32•(-3)4=(-3)6 |
| C、(-a)3•(-a)2=(-a)5 |
| D、(-a)3•(-a)3=a6 |
已知点O是△ABC的外心,且∠ABC+∠ACB=100°,则∠BOC=( )
| A、100° |
| B、100°或80° |
| C、130° |
| D、160° |
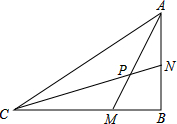 如图,△ABC是直角三角形,CM=AB,BM=AN,求∠CPM.
如图,△ABC是直角三角形,CM=AB,BM=AN,求∠CPM.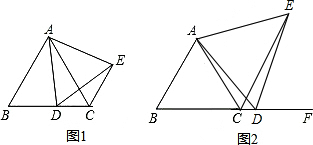 如图①,△ABC是等边三角形,D是BC边上的一点(点D与B、C两点不重合),连接AD,以AD为一边向右侧作等边三角形△ADE,连接CE.
如图①,△ABC是等边三角形,D是BC边上的一点(点D与B、C两点不重合),连接AD,以AD为一边向右侧作等边三角形△ADE,连接CE. 如图,点G是线段EF的中点,则EG=
如图,点G是线段EF的中点,则EG=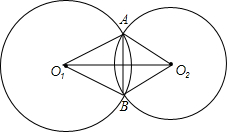 如图,⊙O1与⊙O2相交于A,B两点,连接O1A,O1B,O2A,O2B,得到四边形O1AO2B,连接O1O2,则O1O2垂直平分AB,请说明理由.
如图,⊙O1与⊙O2相交于A,B两点,连接O1A,O1B,O2A,O2B,得到四边形O1AO2B,连接O1O2,则O1O2垂直平分AB,请说明理由. 如图,∠ABD=∠BCD=90°,BC=6,CD=8,当AB=
如图,∠ABD=∠BCD=90°,BC=6,CD=8,当AB=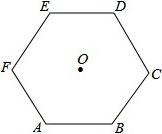 如图,O是正六边形ABCDEF的中心,半径为Rcm,求它的周长L和面积S.
如图,O是正六边形ABCDEF的中心,半径为Rcm,求它的周长L和面积S.