题目内容
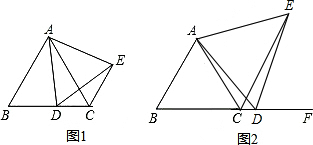 如图①,△ABC是等边三角形,D是BC边上的一点(点D与B、C两点不重合),连接AD,以AD为一边向右侧作等边三角形△ADE,连接CE.
如图①,△ABC是等边三角形,D是BC边上的一点(点D与B、C两点不重合),连接AD,以AD为一边向右侧作等边三角形△ADE,连接CE.(1)求证:CE=BD;
(2)若点D在BC的延长线上运动而题设其他条件不变(如图②),则AB与CE会保持有怎样的位置关系?请证明你的结论.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)易证∠BAD=∠CAE,AB=AC,AD=AE,即可证明△ABD≌△ACE,可得CE=BD,即可解题;
(2)易证∠BAD=∠CAE,AB=AC,AD=AE,即可证明△ABD≌△ACE,可得CE=BD,即可解题.
(2)易证∠BAD=∠CAE,AB=AC,AD=AE,即可证明△ABD≌△ACE,可得CE=BD,即可解题.
解答:证明:(1)∵∠BAD+∠CAD=60°,∠CAE+∠CAD=60°,
∴∠BAD=∠CAE,
∵△ABC、△ADE均为等边三角形,
∴AB=AC,AD=AE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE,(SAS)
∴CE=BD;(2)∵∠BAD=∠CAD+∠BAC=∠CAD+60°,∠CAE=∠CAD+∠DAE=∠CAD+60°,
∴∠BAD=∠CAE,
∵△ABC、△ADE均为等边三角形,
∴AB=AC,AD=AE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴CE=BD.
∴∠BAD=∠CAE,
∵△ABC、△ADE均为等边三角形,
∴AB=AC,AD=AE,
在△ABD和△ACE中,
|
∴△ABD≌△ACE,(SAS)
∴CE=BD;(2)∵∠BAD=∠CAD+∠BAC=∠CAD+60°,∠CAE=∠CAD+∠DAE=∠CAD+60°,
∴∠BAD=∠CAE,
∵△ABC、△ADE均为等边三角形,
∴AB=AC,AD=AE,
在△ABD和△ACE中,
|
∴△ABD≌△ACE(SAS),
∴CE=BD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABD≌△ACE是解题的关键.

练习册系列答案
相关题目
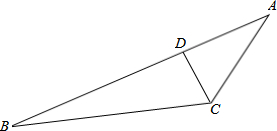 如图,在△ABC中,∠A=2∠B,CD是∠ACB的平分线,则下列各式正确的是( )
如图,在△ABC中,∠A=2∠B,CD是∠ACB的平分线,则下列各式正确的是( )| A、AD=BC-CA |
| B、AD=BC-CD |
| C、BD=AC+CD |
| D、AC=BD-AD |
 已知:如图,AB是⊙O直径,弦CD⊥AB,E为CD延长线上一点,连结BE交圆于F.求证:CF•DE=BC•EF.
已知:如图,AB是⊙O直径,弦CD⊥AB,E为CD延长线上一点,连结BE交圆于F.求证:CF•DE=BC•EF. 如图,△ADC内接于⊙O,且∠EAC=∠D,求证;AE是⊙O的切线.
如图,△ADC内接于⊙O,且∠EAC=∠D,求证;AE是⊙O的切线. 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OA于D,G,交OB于点E,连接DE并延长DE交AB于F,且DE⊥AB
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OA于D,G,交OB于点E,连接DE并延长DE交AB于F,且DE⊥AB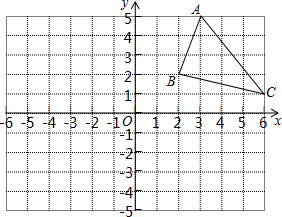 如图,△ABC的顶点坐标分别是A(2,2)、B(3,5)、C(6,1)
如图,△ABC的顶点坐标分别是A(2,2)、B(3,5)、C(6,1)