Question

12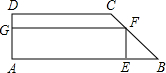．如图，有一块梯形铁板ABCD，AB∥CD，∠A=90°，AB=6m，CD=4m，AD=2m，现在梯形中裁出一内接矩形铁板AEFG，使E在AB上，F在BC上，G在AD上，
（1）若矩形铁板的面积为5m²，则矩形的一边EF长为多少？
（2）矩形铁板的面积会等于10m²吗？若会，请求出此时矩形的一边EF的长；若不会，请说明理由．

Answer 1

分析 （1）作CH⊥AB于H，由条件可以得出四边形ADCH为矩形，根据矩形的性质就可以求出CH、BH的长，设EF=x，则BE=x，AE=6-x，根据矩形的面积公式就可以建立等式，从而求出其解；
（2）利用（1）建立方程．

解答 解：（1）过C作CH⊥AB于H．
在直角梯形ABCD中，DC∥AB，∠ADC=90°，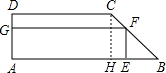

∴四边形ADCH为矩形．
∴CH=AD=2m，BH=AB-CD=6-4=2m．
∴CH=BH．
设EF=x，则BE=x，AE=6-x，由题意，得
x（6-x）=5
整理得：x²-6x+5=0，
（x-1）（x-5）=0，
解得：x₁=1，x₂=5（舍去）
∴矩形的一边EF长为1m．
（2）不会，
理由：由题意得，
x（6-x）=10
整理得：x²-6x-10=0，
解得：x₁=3+$\sqrt{19}$，x₂=3-$\sqrt{19}$，
两根都不合题意，
也就是矩形铁板的面积不会等于10m²．

点评 本题考查了一元二次方程的实际运用，直角梯形的性质，矩形的性质，矩形的面积公式的运用，在解答时根据面积建立方程求解是解决问题的关键．