题目内容
3.利用换元法解下列方程(1)(x2-2x)2+(x2-2x)-2=0;
(2)(2-3x)+(3x-2)2=0.
分析 (1)把x2-2x当成一个整体,用y来代换,原方程可变为:y2+y-2=0,解这个方程,再还原成x2-2x求解;
(2)设m=3x-2,原方程可变为:m2-m=0,解此方程可得m的值,再还原成3x-2求解可得.
解答 解:(1)设y=x2-2x,原方程可变为:y2+y-2=0
解得:y=-2或y=1,即x2-2x=-2或x2-2x=1.
当x2-2x=-2时,△<0,没实数根,
当x2-2x=1时,解得x=1±$\sqrt{2}$.
故原方程的根是x1=1+$\sqrt{2}$,x2=1-$\sqrt{2}$.
(2)设m=3x-2,原方程可变为:m2-m=0,
解得:m=0或m=1,
当m=0时,可得3x-2=0,解得:x=$\frac{2}{3}$,
当m=1时,可得3x-2=1,解得:x=1,
故原方程的根是x1=$\frac{2}{3}$,x2=1.
点评 本题考查了用换元法解分式方程,解题关键是能准确的找出可用替换的代数式,再用字母y代替解方程.

练习册系列答案
相关题目
15.下列各数中,最小的实数是( )
| A. | 0 | B. | π | C. | -$\sqrt{2}$ | D. | -1 |
13.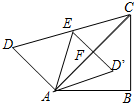 如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )
如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )
 如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )
如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )| A. | $3+\sqrt{3}$ | B. | $3\sqrt{2}+\sqrt{6}$ | C. | $3\sqrt{2}-\sqrt{6}$ | D. | $3-\sqrt{3}$ |
 将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B的对应点E落在坐标平面内,当△ADE是等腰直角三角形时,点E的坐标为(0,1).
将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B的对应点E落在坐标平面内,当△ADE是等腰直角三角形时,点E的坐标为(0,1).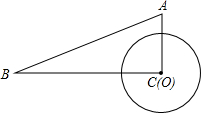 如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,⊙O的圆心在线段CA上,且它的半径为3.
如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,⊙O的圆心在线段CA上,且它的半径为3.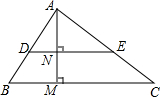 如图,已知△ADE∽△ABC,且AD=3,BD=2.若AM⊥BC于M,AM交DE于N,AM=4,则AN=$\frac{12}{5}$.
如图,已知△ADE∽△ABC,且AD=3,BD=2.若AM⊥BC于M,AM交DE于N,AM=4,则AN=$\frac{12}{5}$.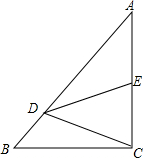 如图,在Rt△ABC中,∠ACB=90°,点D在边AB上,线段DC绕点D按逆时针旋转,端点C恰巧落在边AC上的点E处,已知$\frac{AD}{DB}$=4,求$\frac{AE}{EC}$的值.
如图,在Rt△ABC中,∠ACB=90°,点D在边AB上,线段DC绕点D按逆时针旋转,端点C恰巧落在边AC上的点E处,已知$\frac{AD}{DB}$=4,求$\frac{AE}{EC}$的值.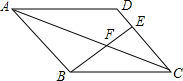 如图,在平行四边形ABCD中,E在DC上,若BF:BE=4:7,则DE:EC=1:3.
如图,在平行四边形ABCD中,E在DC上,若BF:BE=4:7,则DE:EC=1:3.