题目内容
18.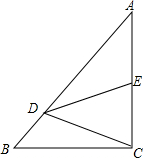 如图,在Rt△ABC中,∠ACB=90°,点D在边AB上,线段DC绕点D按逆时针旋转,端点C恰巧落在边AC上的点E处,已知$\frac{AD}{DB}$=4,求$\frac{AE}{EC}$的值.
如图,在Rt△ABC中,∠ACB=90°,点D在边AB上,线段DC绕点D按逆时针旋转,端点C恰巧落在边AC上的点E处,已知$\frac{AD}{DB}$=4,求$\frac{AE}{EC}$的值.
分析 作DH⊥AC于H,由旋转的性质得出DE=DC,得出EH=CH,设$\frac{AE}{EC}$=n,即AE=nEC,因此AE=2nEH=2nCH,证明DH∥BC,得出△ADH∽△ABC,得出比例式$\frac{AB}{AD}$=$\frac{AC}{AH}$,求出n的值,即可得出结果.
解答 解:作DH⊥AC于H,如图所示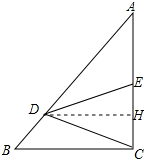
∵线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处,
∴DE=DC,
∴EH=CH,
设$\frac{AE}{EC}$=n,即AE=nEC,
∴AE=2nEH=2nCH,
∵∠C=90°,
∴DH∥BC,
∴△ADH∽△ABC,
∴$\frac{AB}{AD}$=$\frac{AC}{AH}$,
∵$\frac{AD}{DB}$=4,
∴$\frac{AB}{AD}$=$\frac{5}{4}$,
∴$\frac{AC}{AH}$=$\frac{5}{4}$,即$\frac{AE+EC}{AE+EH}$=$\frac{2nCH+2CH}{2nCH+CH}$=$\frac{5}{4}$,
解得:n=1.5,
∴$\frac{AE}{EC}$=$\frac{3}{2}$.
点评 本题考查了相似三角形的判定与性质、旋转的性质、等腰三角形的性质等知识;熟练掌握相似三角形的判定与性质是解决问题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
8.下列事件中,是不可能事件的是( )
| A. | 买一张电影票,座位号是偶数 | B. | 度量三角形的内角和,结果是360° | ||
| C. | 明天会下雨 | D. | 设计运动员射击一次,命中8环 |
10. 如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )
如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )
 如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )
如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
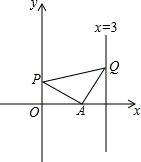 如图,在平面直角坐标系xOy中,点A的坐标为(2,0),Q是直线x=3上的一个动点,y轴正半轴上是否存在点P,使△APQ为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
如图,在平面直角坐标系xOy中,点A的坐标为(2,0),Q是直线x=3上的一个动点,y轴正半轴上是否存在点P,使△APQ为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.