题目内容
11.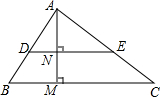 如图,已知△ADE∽△ABC,且AD=3,BD=2.若AM⊥BC于M,AM交DE于N,AM=4,则AN=$\frac{12}{5}$.
如图,已知△ADE∽△ABC,且AD=3,BD=2.若AM⊥BC于M,AM交DE于N,AM=4,则AN=$\frac{12}{5}$.
分析 由相似三角形的性质得出对应高的比等于相似比,即可得出结果.
解答 解:∵AD=3,BD=2,
∴AB=5,
∵△ADE∽△ABC,AM⊥BC于M,
∴$\frac{AN}{AM}=\frac{AD}{AB}$=$\frac{3}{5}$,
即$\frac{AN}{4}=\frac{3}{5}$,
解得:AN=$\frac{12}{5}$;
故答案为:$\frac{12}{5}$.
点评 本题考查了相似三角形的性质;熟记相似三角形对应高的比等于相似比是解决问题的关键.

练习册系列答案
相关题目
1.代数式2abc,-3x2+x,-$\frac{3}{x}$,2$\frac{1}{3}$中,单项式的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.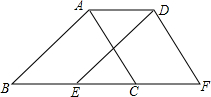 如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )
如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )
 如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )
如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
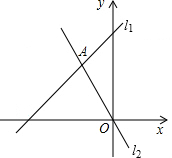 如图,直线l1:y=kx+b与l2:y=-2x相交于A(-2,4),那么不等式kx+b>-2x的解集为x>-2.
如图,直线l1:y=kx+b与l2:y=-2x相交于A(-2,4),那么不等式kx+b>-2x的解集为x>-2.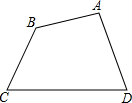 如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗?
如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗? 如图,已知:点E是正方形ABCD的BC边上的点,现将△DCE沿折痕DE向上翻折,使DC落在对角线DB上,则CD:CE==($\sqrt{2}$+1):1.
如图,已知:点E是正方形ABCD的BC边上的点,现将△DCE沿折痕DE向上翻折,使DC落在对角线DB上,则CD:CE==($\sqrt{2}$+1):1.