题目内容
13. 将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B的对应点E落在坐标平面内,当△ADE是等腰直角三角形时,点E的坐标为(0,1).
将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B的对应点E落在坐标平面内,当△ADE是等腰直角三角形时,点E的坐标为(0,1).
分析 由矩形的性质和已知条件得出BD=3,由折叠的性质得出AB=AE,BD=DE,∠ABD=∠AED=90°,当△ADE是等腰直角三角形时,AE=ED,得出AB=BD,∠BAD=45°,因此∠DAE=∠BAD=45°,得出AB=BD=AE=DE=3,证出四边形ABDE是正方形,OE=1,即可得出结果.
解答 解:∵四边形OABC为矩形,点A的坐标为(0,4),点D的坐标为(m,1),
∴BD=3,
∵将矩形OABC沿AD折叠压平,使点B的对应点E落在坐标平面内,
∴AB=AE,BD=DE,∠ABD=∠AED=90°,
∵当△ADE是等腰直角三角形时,AE=ED,
∴AB=BD,∠BAD=45°,
∴∠DAE=∠BAD=45°,
∴E在y轴上,AB=BD=AE=DE=3,
∴四边形ABDE是正方形,OE=1,
∴点E的坐标为(0,1);
故答案为:(0,1).
点评 本题考查了矩形的性质、等腰直角三角形的性质、正方形的判定与性质、坐标与图形性质;熟练掌握矩形得性质和折叠的性质,证出四边形是正方形是解决问题的关键.

练习册系列答案
相关题目
1.代数式2abc,-3x2+x,-$\frac{3}{x}$,2$\frac{1}{3}$中,单项式的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.下列事件中,是不可能事件的是( )
| A. | 买一张电影票,座位号是偶数 | B. | 度量三角形的内角和,结果是360° | ||
| C. | 明天会下雨 | D. | 设计运动员射击一次,命中8环 |
18.按某种标准把多项式分类,4x2-4与a3b+2ab2属于同一类,则下列多项式中也属于这一类的是( )
| A. | -x5+y3 | B. | 3x3+x+1 | C. | 2ab+cd+2 | D. | a4+3a3+2ab2+b3 |
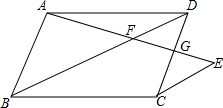 已知:如图,在?ABCD中,AE与对角线BD相交于点F,EF=AF.
已知:如图,在?ABCD中,AE与对角线BD相交于点F,EF=AF.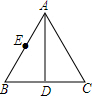 如图,已知AD是等边△ABC的角平分线,点E是AB的中点,且AD=6,BD=2,点M是AD上一动点,求△BEM的周长的最小值.
如图,已知AD是等边△ABC的角平分线,点E是AB的中点,且AD=6,BD=2,点M是AD上一动点,求△BEM的周长的最小值.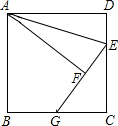 如图,正方形ABCD中,点E在边CD上,将△ADE沿AE翻折至△AFE,延长EF交边BC于点G,若点E是CD中点,则BG:CG=1:2.
如图,正方形ABCD中,点E在边CD上,将△ADE沿AE翻折至△AFE,延长EF交边BC于点G,若点E是CD中点,则BG:CG=1:2.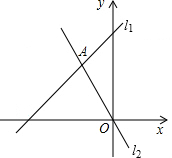 如图,直线l1:y=kx+b与l2:y=-2x相交于A(-2,4),那么不等式kx+b>-2x的解集为x>-2.
如图,直线l1:y=kx+b与l2:y=-2x相交于A(-2,4),那么不等式kx+b>-2x的解集为x>-2.