题目内容
13.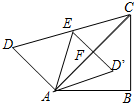 如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )
如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )| A. | $3+\sqrt{3}$ | B. | $3\sqrt{2}+\sqrt{6}$ | C. | $3\sqrt{2}-\sqrt{6}$ | D. | $3-\sqrt{3}$ |
分析 连接CD′,BD′,过点D′作D′G⊥BC于点G,进而得出△ABD′≌△CBD′,于是得到∠D′BG=45°,D′G=GB,进而利用勾股定理求出点D′到BC边的距离.
解答 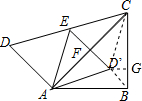 解:连接CD′,BD′,过点D′作D′G⊥BC于点G,
解:连接CD′,BD′,过点D′作D′G⊥BC于点G,
∵AC垂直平分线ED′,
∴AE=AD′,CE=CD′,
∵AE=EC,∴AD′=CD′=4$\sqrt{3}$,
在△ABD′和△CBD′中,
$\left\{\begin{array}{l}{AB=BC}\\{BD′=BD′}\\{AD′=CD′}\end{array}\right.$,
∴△ABD′≌△CBD′(SSS),
∴∠D′BG=45°,
∴D′G=GB,
设D′G长为xcm,则CG长为(6$\sqrt{2}$-x)cm,
在Rt△GD′C中
x2+(6$\sqrt{2}$-x)2=(4$\sqrt{3}$)2,
解得:x1=3$\sqrt{2}$-$\sqrt{6}$,x2=3$\sqrt{2}$+$\sqrt{6}$(舍去),
∴点D′到BC边的距离为(3$\sqrt{2}$-$\sqrt{6}$)cm.
故选C.
点评 此题主要考查了折叠的性质,全等三角形的判定与性质和锐角三角函数关系以及等边三角形的判定与性质等知识,利用垂直平分线的性质得出点E,D′关于直线AC对称是解题关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
4.若x=-2是方程2x-5m=6的解,则m的值为( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
1.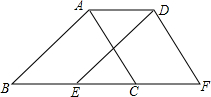 如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )
如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )
 如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )
如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
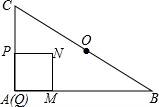 如图,在Rt△ABC中,AB=4,AC=3,点O为BC的中点,点P从点A出发,沿折线AC-CO以每秒1个单位长度的速度向终点O运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图,在Rt△ABC中,AB=4,AC=3,点O为BC的中点,点P从点A出发,沿折线AC-CO以每秒1个单位长度的速度向终点O运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒). 平行四边形ABCD的周长为24,对角线AC、BD相交于点O,作OE⊥AC,交AD与点E,连接CE,那么△DEC的周长为12.
平行四边形ABCD的周长为24,对角线AC、BD相交于点O,作OE⊥AC,交AD与点E,连接CE,那么△DEC的周长为12.