题目内容
12.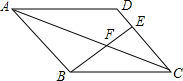 如图,在平行四边形ABCD中,E在DC上,若BF:BE=4:7,则DE:EC=1:3.
如图,在平行四边形ABCD中,E在DC上,若BF:BE=4:7,则DE:EC=1:3.
分析 求出BF:EF=4:3,根据平行四边形的性质得出AB=DC,AB∥DC,根据相似三角形的判定得出△CEF∽△ABF,求出$\frac{AB}{CE}$=$\frac{4}{3}$,即可得出答案.
解答 解:∵BF:BE=4:7,
∴BF:EF=4:3,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴△CEF∽△ABF,
∴$\frac{BF}{EF}$=$\frac{AB}{CE}$=$\frac{4}{3}$,
∴CE:CD=3:4,
∴DE:EC=1:3,
故答案为:1:3.
点评 本题考查了平行四边形的性质,相似三角形的性质和判定的应用,能求出$\frac{AB}{CE}$=$\frac{4}{3}$是解此题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
17.抛物线y=-x2+2x-3的对称轴是直线( )
| A. | x=1 | B. | x=-1 | C. | x=2 | D. | x=-2 |
4.若x=-2是方程2x-5m=6的解,则m的值为( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
1.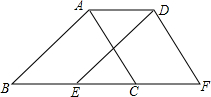 如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )
如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )
 如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )
如图,将周长为9的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
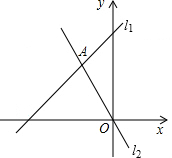 如图,直线l1:y=kx+b与l2:y=-2x相交于A(-2,4),那么不等式kx+b>-2x的解集为x>-2.
如图,直线l1:y=kx+b与l2:y=-2x相交于A(-2,4),那么不等式kx+b>-2x的解集为x>-2. 如图,已知:点E是正方形ABCD的BC边上的点,现将△DCE沿折痕DE向上翻折,使DC落在对角线DB上,则CD:CE==($\sqrt{2}$+1):1.
如图,已知:点E是正方形ABCD的BC边上的点,现将△DCE沿折痕DE向上翻折,使DC落在对角线DB上,则CD:CE==($\sqrt{2}$+1):1. 平行四边形ABCD的周长为24,对角线AC、BD相交于点O,作OE⊥AC,交AD与点E,连接CE,那么△DEC的周长为12.
平行四边形ABCD的周长为24,对角线AC、BD相交于点O,作OE⊥AC,交AD与点E,连接CE,那么△DEC的周长为12.