题目内容
17.正数a,b,c,d满足a+b+c+d=100,$\frac{a}{b+c+d}$+$\frac{b}{a+c+d}$+$\frac{c}{a+b+d}$+$\frac{d}{a+b+c}$=95,则$\frac{1}{b+c+d}$+$\frac{1}{a+c+d}$+$\frac{1}{a+b+d}$+$\frac{1}{a+b+c}$=$\frac{49}{50}$.分析 要求分式的分母比较大,通分会很麻烦.可通过a+b+c+d=100,变形等式里的分式,$\frac{a}{b+c+d}=\frac{100-(b+c+d)}{b+c+d}$=$\frac{100}{b+c+d}-1$,利用整体代入的方法.
解答 解:因为a+b+c+d=100,
所以$\frac{a}{b+c+d}$+$\frac{b}{a+c+d}$+$\frac{c}{a+b+d}$+$\frac{d}{a+b+c}$=95可变形为
$\frac{100-(b+c+d)}{b+c+d}$+$\frac{100-(a+c+d)}{a+c+d}$+$\frac{100-(a+b+d)}{a+b+d}$+$\frac{100-(a+b+c)}{a+b+c}$=95
即$\frac{100}{b+c+d}-1$+$\frac{100}{a+c+d}$-1+$\frac{100}{a+b+d}-1$+$\frac{100}{a+b+c}$-1=95
所以$\frac{100}{b+c+d}$+$\frac{100}{a+c+d}$+$\frac{100}{a+b+d}$+$\frac{100}{a+b+c}$=95
所以$\frac{1}{b+c+d}+\frac{1}{a+c+d}+\frac{1}{a+b+d}+\frac{1}{a+b+c}=\frac{49}{50}$
故答案为:$\frac{49}{50}$
点评 本题考查了分式的加减,等式的变形及分式除法的相关知识.利用a+b+c+d=100,变形$\frac{a}{b+c+d}$+$\frac{b}{a+c+d}$+$\frac{c}{a+b+d}$+$\frac{d}{a+b+c}$=95是解决本题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 2016 | B. | -2017 | C. | -2016 | D. | 2017 |
| A. | 1-x是一次单项式 | B. | 单项式a的系数和次数都是1 | ||
| C. | 2m-(2m+n)的运算结果为4m-n | D. | 单项式2×104x2的系数是2 |
 如图,△ABC的顶点都是正方形网格中的格点,则tan∠ABC等于( )
如图,△ABC的顶点都是正方形网格中的格点,则tan∠ABC等于( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 2 |

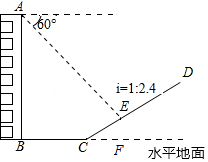 如图,一楼房AB后有一小山坡,其坡度为i=1:2.4,山坡坡面上E点处有一亭子,测得山坡脚C与楼房水平距离BC=30米,与亭子距离CE=26米,小丽从楼房顶测得E点的俯角为60°,求楼房AB的高.
如图,一楼房AB后有一小山坡,其坡度为i=1:2.4,山坡坡面上E点处有一亭子,测得山坡脚C与楼房水平距离BC=30米,与亭子距离CE=26米,小丽从楼房顶测得E点的俯角为60°,求楼房AB的高.