题目内容
9.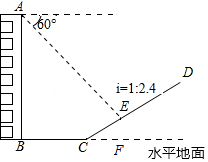 如图,一楼房AB后有一小山坡,其坡度为i=1:2.4,山坡坡面上E点处有一亭子,测得山坡脚C与楼房水平距离BC=30米,与亭子距离CE=26米,小丽从楼房顶测得E点的俯角为60°,求楼房AB的高.
如图,一楼房AB后有一小山坡,其坡度为i=1:2.4,山坡坡面上E点处有一亭子,测得山坡脚C与楼房水平距离BC=30米,与亭子距离CE=26米,小丽从楼房顶测得E点的俯角为60°,求楼房AB的高.注:坡度i是指坡面的铅垂高度与水平宽度的比.
分析 过点E作EF⊥BC的延长线于点F,作EH⊥AB于点H,根据坡度的概念求出EF、CH,根据正切的定义求出AH,计算即可.
解答 解:过点E作EF⊥BC的延长线于点F,作EH⊥AB于点H,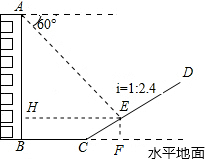
在Rt△CEF中,∵i=CF:EF=$\frac{5}{12}$,CE=26米,
∴EF=10米,CF=24米,
∴BH=EF=10米,HE=BF=BC+CF=54米,
在Rt△AHE中,∵∠HAE=30°,
∴AH=$\frac{EH}{tan30°}$=54$\sqrt{3}$米,
∴AB=AH+HB=(10+54$\sqrt{3}$)米.
答:楼房AB的高为(10+54$\sqrt{3}$)米.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度坡角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
19.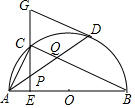 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是( )
如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是( )
 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是( )
如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是( )| A. | ①③⑤ | B. | ②④⑤ | C. | ①②⑤ | D. | ①③④ |
1.到三角形三边距离相等的点是( )
| A. | 三角形的两条平分线的交点 | |
| B. | 三角形的两条高的交点 | |
| C. | 三角形的三条中线的交点 | |
| D. | 三角形的三条边的垂直平分线的交点 |
19. 如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
 如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )| A. | k1>k2>k3 | B. | k2>k1>k3 | C. | k3>k2>k1 | D. | k3>k1>k2 |

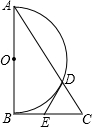 如图,Rt△ABC中,∠ABC=90°,以AB的中点O为圆心、OA长为半径作半圆,交AC于点D,点E为BC的中点,连接DE.
如图,Rt△ABC中,∠ABC=90°,以AB的中点O为圆心、OA长为半径作半圆,交AC于点D,点E为BC的中点,连接DE.