题目内容
7.已知y-1与x-4成正比例,当x=5时,y=3,写出y与x之间的函数关系式y=2x-7.分析 根据y-1与x-4成正比例可设y-1=k(x-4),再把当x=5时,y=3代入求出k的值即可.
解答 解:∵y-1与x-4成正比例,
∴设y-1=k(x-4),
∵当x=5时,y=3,
∴3-1=k(5-4),解得k=2,
∴y-1=2(x-4),
∴y=2x-7.
故答案为:y=2x-7.
点评 本题考查的是待定系数法求一次函数的解析式,根据题意得出k的值是解答此题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
2.下列运算正确的是( )
| A. | 2÷$\sqrt{2}$=$\frac{1}{2}$ | B. | $\sqrt{(-2)^{2}}$=-2 | C. | (-$\sqrt{2}$)2=-2 | D. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ |
12.将抛物线y=x2向右平移1个单位长度,再向上平移2个单位长度所得的抛物线解析式为( )
| A. | y=(x-1)2+2 | B. | y=(x+1)2+2 | C. | y=(x-1)2-2 | D. | y=(x+1)2-2 |
19. 如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
 如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )| A. | k1>k2>k3 | B. | k2>k1>k3 | C. | k3>k2>k1 | D. | k3>k1>k2 |
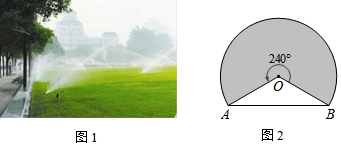
16.如图(1)是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是如图(2)所示的扇形.如果A,B两点的距离为18m,那么这种装置能够喷灌的草坪面积为72πm2.

17.若直角三角形两边长分别是6,8,则它的斜边为( )
| A. | 8 | B. | 10 | C. | 8或10 | D. | 以上都不正确 |
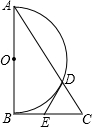 如图,Rt△ABC中,∠ABC=90°,以AB的中点O为圆心、OA长为半径作半圆,交AC于点D,点E为BC的中点,连接DE.
如图,Rt△ABC中,∠ABC=90°,以AB的中点O为圆心、OA长为半径作半圆,交AC于点D,点E为BC的中点,连接DE.