题目内容
将一张长方形的纸对折，如图所示，可得到一条折痕（图中虚线），继续对折，对折时每次折痕与上次的折痕保持平行，连续对折三次后，可以得到7条折痕，那么如果对折五次，可以得到 条折痕，对折n次可以得到 条折痕．
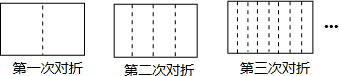
考点：规律型：图形的变化类
专题：
分析：利用已知得出折痕的条数的变化规律，进而求出答案．
解答：解：∵对折一次后有21-1=1条折痕，对折二次后有22-1=3条折痕，对折三次后有23-1=7条折痕，
∴对折五次，可以得到25-1=31条折痕，故对折n次可以得到2n-1条折痕．
故答案为：31，2n-1．
∴对折五次，可以得到25-1=31条折痕，故对折n次可以得到2n-1条折痕．
故答案为：31，2n-1．
点评：此题主要考查了图形的变化类，得出折痕的变化规律是解题关键．
练习册系列答案
相关题目
如图，直角坐标系内的梯形AOBC，AC∥OB，AC、OB的长分别是关于x的方程x2-6mx+m2+4=0的两根，并且S△AOC：S△BOC=1：5．
如图，为了测量某建筑物的高AB，在距离点B25米的D处安置测角仪，测得点A的仰角α为71°6′，已知仪器的高CD=1.52米，求建筑物的高AB．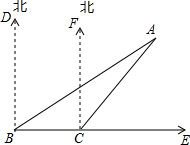
如图，一艘渔船在B处测得灯塔A在北偏东60°的方向，另一艘货轮在C处测得灯塔A在北偏东40°的方向，那么在灯塔A处观看B和C时的视角∠BAC是多少度？
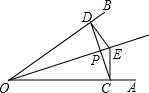如图，点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别是C，D．下列结论中正确的有（ ）
已知：如图，CB⊥BE于B，ED⊥CD于D，BE、CD交于点A，并且AB=AD，求证：△ABC≌△ADE．