题目内容
在下列长度的四根木棒中，能与4cm、9cm长的两根木棒钉成一个三角形的是（ ）
A. 4cm B. 5cm C. 9cm D. 13cm
C
【解析】试题解析：根据三角形的三边关系，得：第三边应大于两边之差，且小于两边之和，
即9-4=5，9+4=13．
∴第三边取值范围应该为：5＜第三边长度＜13，
故只有C选项符合条件．
故选C．
练习册系列答案
习题精选系列答案
相关题目
如图，△ABC中，D、E在AB上，且D、E分别是AC、BC的垂直平分线上一点．
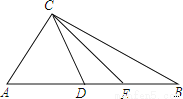
（1）若△CDE的周长为4，求AB的长；
（2）若∠ACB=100°，求∠DCE的度数；
（3）若∠ACB=a（90°＜a＜180°），则∠DCE=___________.
（1）4；（2）20°；（3）2α-180°.
【解析】试题分析：（1）根据线段的垂直平分线的性质得到DC=DA，EC=EB，根据三角形的周长公式计算即可；
（2）根据三角形内角和定理求出∠A+∠B的度数，根据等腰三角形的性质求出∠DCA+∠ECB，根据题意计算即可；
（3）根据（2）的方法解答．
试题解析：（1）∵D、E分别是AC、BC的垂直平分线上一点，
∴DC=... 如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,指出其他的对应边和对应角.
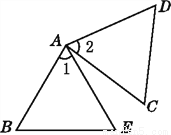
见解析
【解析】试题分析：先根据△ABE≌△ACD，可以确定点A的对应点是A，点B的对应点是C，点D的对应点是E，然后根据对应顶点，结合图形即可找出对应边和对应角.
试题解析：∵△ABE≌△ACD，∠1=∠2，∠B=∠C，
∴点A的对应点是A，点B的对应点是C，点E的对应点是D，
∴∠BAE与∠CAD是对应角，AB与AC，BE与CD，AD与AE是对应边. 如图，在△ABC中，BD是边AC上的中线，E是BC的中点，连接DE.如果△BDE的面积为2，那么△ABC的面积为______．
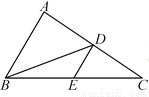
8
【解析】∵E是BC的中点,
∴ ,
∵BD是边AC上的中线,
∴ ,
∴,
又△BDE的面积为2，
∴△ABC的面积为8；
故答案是：8. 如图，∠A＝∠B，∠C＝α，DE⊥AC，FD⊥AB，则∠EDF等于( )
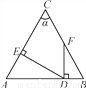
A. α B. 90°－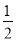
α C. 90°－α D. 180°－2α
B
【解析】∵∠A=∠B，∠C=α，
∴∠A=∠B=（180°-α），
∵DE⊥AC，FD⊥AB，
∴∠AED=∠FDB=90°，
∴∠ADE=90°-（180°-α）=α，
∴∠EDF =180°-90°-α=90°-α，
故选B． [(2x－y)(2x＋y)＋y(y－6x)＋x(6y－2)]÷2x，其中x＝1009.
2017
【解析】试题分析：先计算中括号内的式子，把结果化为最简后，再利用多项式除以单项式的运算法则计算，最后代入求值即可.
试题解析：
[(2x－y)(2x＋y)＋y(y－6x)＋x(6y－2)]÷2x，
=
=
=2x-1
当x＝1009时，原式=2018-1=2017. 单项式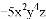
的系数是________，次数是 _______.
-5 7
【解析】单项式中的数字因数是单项式的系数，所有字母的指数的和叫做这个单项式的次数.由此可得单项式的系数是-5，次数是7. (2x－y)2·(2x＋y)2
16x4－8x2y2＋y4
【解析】试题分析：根据积的乘方的运算法则把(2x－y)2·(2x＋y)2转化为后，先利用平方差公式计算，再利用完全平方公式计算即可.
试题解析：
(2x－y)2·(2x＋y)2
=
=
=16x4－8x2y2＋y4 下列方程中，解为x=-3的方程是（ ）
A.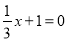 
B. 2x-1=8-x C. -3x=1 D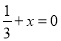
A
【解析】试题分析：A、把x＝－3代入方程x＋1＝0得：左边＝0，右边＝0，
左边＝右边，
所以x＝－3是方程的解，故本选项符合题意；
B、把x＝－3代入方程2x－1＝8－x得：左边＝－7，右边＝11，
左边≠右边，
所以x＝－3不是方程的解，故本选项不符合题意；
C、把x＝－3代入方程－3x＝1得：左边＝9，右边＝1，
左边≠右边，
所以x...