题目内容
[(2x－y)(2x＋y)＋y(y－6x)＋x(6y－2)]÷2x，其中x＝1009.
2017
【解析】试题分析：先计算中括号内的式子，把结果化为最简后，再利用多项式除以单项式的运算法则计算，最后代入求值即可.
试题解析：
[(2x－y)(2x＋y)＋y(y－6x)＋x(6y－2)]÷2x，
=
=
=2x-1
当x＝1009时，原式=2018-1=2017.
练习册系列答案
阅读快车系列答案
相关题目
如图，已知线段AB的垂直平分线CP交AB于点P，且AP=2PC，现欲在线段AB上求作两点D，E，使其满足AD=DC=CE=EB，对于以下甲、乙两种作法：
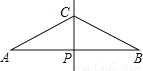
甲：分别作∠ACP、∠BCP的平分线，分别交AB于D、E，则D、E即为所求；乙：分别作AC、BC的垂直平分线，分别交AB于D、E，则D、E两点即为所求．下列说法正确的是（ ）
A. 甲、乙都正确 B. 甲、乙都错误
C. 甲正确，乙错误 D. 甲错误，乙正确
D
【解析】试题解析：甲：虽然CP=AP，
但∠A≠∠ACP，
即∠A≠∠ACD．甲不正确；
乙∵CP是线段AB的中垂线，
∴△ABC是等腰三角形，即AC=BC，∠A=∠B，
作AC、BC之中垂线分别交AB于D、E，
∴∠A=∠ACD，∠B=∠BCE，
∵∠A=∠B，
∴∠A=∠ACD，∠B=∠BCE，
∵AC=BC，
∴△ACD≌... 若△ABC与△DEF全等,点A和点E,点B和点D分别是对应点,则下列结论错误的是( )
A. BC=EF B. ∠B=∠D
C. ∠C=∠F D. AC=EF
A
【解析】∵点A和点E，点B和点D分别是对应点，
∴△ABC≌△EDF，
∴∠A=∠E，∠B=∠D，∠C=∠F，AC=EF，BC=DF，AB=ED.
故选：A. 如图，直线l1∥l2，若∠1=130°，∠2=60°，则∠3= ．
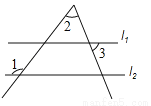
70°．
【解析】
试题分析：∵直线l1∥l2，∴∠4=∠1=130°，∴∠5=∠4﹣∠2=70°，∴∠5=∠3=70°．，故答案为：70°． 在下列长度的四根木棒中，能与4cm、9cm长的两根木棒钉成一个三角形的是（ ）
A. 4cm B. 5cm C. 9cm D. 13cm
C
【解析】试题解析：根据三角形的三边关系，得：第三边应大于两边之差，且小于两边之和，
即9-4=5，9+4=13．
∴第三边取值范围应该为：5＜第三边长度＜13，
故只有C选项符合条件．
故选C． 若(2x＋1)0＝1，则x的取值范围是_____.
x≠-
【解析】任何一个不等于零的数的零次幂都等于1.由此可得2x+1≠0，解得，所以当(2x＋1)0＝1，x的取值范围是. 如果x2＋ax＋9＝(x＋3)2，那么a的值为( )
A. 3 B. ±3 C. 6 D. ±6
C
【解析】∵x2+ax+9=（x+3）2，而（x+3）2=x2+6x+9；即x2+ax+9=x2 已知a是－2的相反数，且|b＋1|＝0，则[－3a2(ab2＋2a)＋4a(－ab)2]÷(－4a)的值为_____.
5
【解析】[－3a2(ab2＋2a)＋4a(－ab)2]÷(－4a)
=
=
=
∵a是－2的相反数，且|b＋1|＝0，
∴a=2，b=-1，
∴原式==-1+6=5. 下面用代数式表示正确的是（ ）
A. -a的平方表示为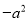
B. a与比a大2的数的积表示为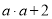
C. a与b的和的平方表示为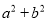
D. a，b两数差的平方表示为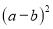
D
【解析】试题分析：A、－a的平方表示为(－a)2，故此选项错误；
B、a与比a大2的数的积表示为a(a＋2)，故此选项错误；
C、a与b的和的平方表示为(a＋b)2，故此选项错误；
D、a，b两数差的平方表示为(a－b)2，故此选项错误．
故选D．