题目内容
4. 画图并填空:
画图并填空:如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.
(1)画出平移后的△A′B′C′,(利用网格点和三角板画图)
(2)画出AB边上的高线CD;
(3)画出BC边上的中线AE;
(4)在平移过程中高CD扫过的面积为16.(网格中,每一小格单位长度为1).
分析 (1)连接BB′,过A、C分别做BB′的平行线,并且在平行线上截取AA′=CC′=BB′,顺次连接平移后各点,得到的三角形即为平移后的三角形;
(2)从C点向AB的作垂线,垂足为点D,CD即为AB边上的高;
(3)找到BC的中点E,连接AE,AE就是所求的中线;
(4)求出平行四边形DCC'D'的面积即可.
解答 解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:CD即为AB边上的高;
(3)如图所示:AE就是所求的中线;
(4)面积=4×8÷2=16.
故答案为:16.
点评 考查了根据平移变换作图,其中平移作图的一般步骤为:①确定平移的方向和距离,先确定一组对应点;②确定图形中的关键点;③利用第一组对应点和平移的性质确定图中所有关键点的对应点;④按原图形顺序依次连接对应点,所得到的图形即为平移后的图形.同时考查了三角形的中线,高的一些基本画图方法.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
12.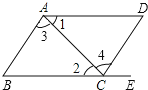 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;其中,能推出AB∥DC的条件为( )
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;其中,能推出AB∥DC的条件为( )
 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;其中,能推出AB∥DC的条件为( )
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;其中,能推出AB∥DC的条件为( )| A. | ①② | B. | ①③ | C. | ②③ | D. | 以上都错 |
9.根据下列条件,能判断出一个四边形是平行四边形的是( )
| A. | 一组对边相等 | B. | 两条对角线互相垂直 | ||
| C. | 一组对边平行 | D. | 两条对角线互相平分 |
13.将一组数据中的每一个数减去40后,所得新的一组数据的平均数是2,则原来那组数据的平均数是( )
| A. | 40 | B. | 42 | C. | 38 | D. | 2 |
14.小华的老师让他在无法看到袋子里小球的情形下,从袋子里摸出一个小球.袋子里各种颜色小球的数量统计如表所示.小华摸到褐色小球的概率为( )
| 颜色 | 红色 | 橙色 | 黄色 | 绿色 | 蓝色 | 紫色 | 褐色 |
| 数量 | 6 | 4 | 3 | 3 | 2 | 2 | 5 |
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
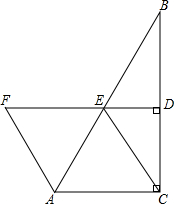 如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF∥CE.
如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF∥CE.