题目内容
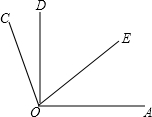 如图,OE为∠AOD的平分线,∠COD=
如图,OE为∠AOD的平分线,∠COD=| 1 |
| 4 |
(1)∠EOD的大小;
(2)∠AOD补角的大小.
考点:余角和补角,角平分线的定义
专题:
分析:(1)利用∠COD的度数,以及∠COD与∠EOC的倍数关系,得出∠EOC的度数,再减去∠COD即可;
(2)根据∠DOE的度数以及角平分线的性质,得出∠AOD的度数,再根据互为补角的定义求即可.
(2)根据∠DOE的度数以及角平分线的性质,得出∠AOD的度数,再根据互为补角的定义求即可.
解答:解:(1)∵∠EOC=4∠COD,∠COD=15°,
∴∠EOC=4∠COD=4×15°=60°,
又∵∠EOD=∠EOC-∠COD,
∴∠EOD=60°-15°=45°
(2)∵OE平分∠AOD,
∴∠AOD=2∠EOD=4×=45°=90°,
∴∠AOD的补角为180°-90°=90°.
∴∠EOC=4∠COD=4×15°=60°,
又∵∠EOD=∠EOC-∠COD,
∴∠EOD=60°-15°=45°
(2)∵OE平分∠AOD,
∴∠AOD=2∠EOD=4×=45°=90°,
∴∠AOD的补角为180°-90°=90°.
点评:本题考查了角平分线的定义,根据角平分线定义得出所求角与已知角的关系转化求解.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
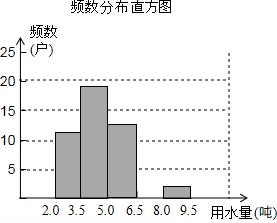 某市在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽取获得的50个家庭去年的月人均用水量(单位:吨)的调查数据进行研究了如下整理:
某市在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽取获得的50个家庭去年的月人均用水量(单位:吨)的调查数据进行研究了如下整理:
 在括号内填写理由.
在括号内填写理由.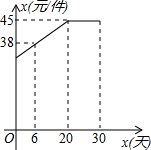 某商人在我县开办了一家儿童服装专卖店,该店在儿童节前5月31日采购进一种今年流行的服装,6月份(6月1日至6月30日)进行30天的试销售,购进价格为20元/件.销售结束后,得知日销售量y(件)与销售时间x(天)之间的函数关系为:
某商人在我县开办了一家儿童服装专卖店,该店在儿童节前5月31日采购进一种今年流行的服装,6月份(6月1日至6月30日)进行30天的试销售,购进价格为20元/件.销售结束后,得知日销售量y(件)与销售时间x(天)之间的函数关系为: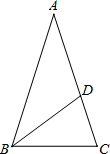 如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x. 图中直线是由直线l向上平移1个单位,向左平移2个单位得到的,则直线l对应的一次函数关系式为
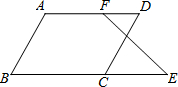
图中直线是由直线l向上平移1个单位,向左平移2个单位得到的,则直线l对应的一次函数关系式为 如图,在梯形ABCD中,AD∥BC,BD=CD,AD=1,BC=8,∠BDC=90°,则AB的长为
如图,在梯形ABCD中,AD∥BC,BD=CD,AD=1,BC=8,∠BDC=90°,则AB的长为