题目内容
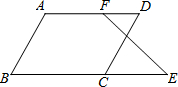 在括号内填写理由.
在括号内填写理由.如图,已知∠B+∠BCD=180°,∠B=∠D.
求证:AD∥BE.
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥
∴∠DCE=∠B(
又∵∠B=∠D( 已知 ),
∴∠DCE=
∴AD∥BE (
考点:平行线的判定与性质
专题:推理填空题
分析:根据平行线的判定推出AB∥CD,根据平行线的性质和已知推出∠DCE=∠D,根据平行线的判定定理推出即可.
解答:证明:∵∠B+∠BCD=180°,
∴AB∥CD(同旁内角互补,两直线平行),
∴∠DEC=∠B(两直线平行,同位角相等),
∵∠B=∠D,
∴∠DCE=∠D,
∴AD∥BE(内错角相等,两直线平行),
故答案为:CD,同旁内角互补,两直线平行,两直线平行,同位角相等,∠D,内错角相等,两直线平行.
∴AB∥CD(同旁内角互补,两直线平行),
∴∠DEC=∠B(两直线平行,同位角相等),
∵∠B=∠D,
∴∠DCE=∠D,
∴AD∥BE(内错角相等,两直线平行),
故答案为:CD,同旁内角互补,两直线平行,两直线平行,同位角相等,∠D,内错角相等,两直线平行.
点评:本题考查了对平行线的性质和判定的应用,主要考查学生的推理能力,题目比较好,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知△ACF≌△DBE,AD=9厘米,BC=5厘米,求AB的长.
如图,已知△ACF≌△DBE,AD=9厘米,BC=5厘米,求AB的长. 如图,某居民小区有一长方形地,居民想在长方形地内修筑同样宽的两条小路,余下部分绿化,道路的宽为2米,则绿化的面积为多少平方米?
如图,某居民小区有一长方形地,居民想在长方形地内修筑同样宽的两条小路,余下部分绿化,道路的宽为2米,则绿化的面积为多少平方米?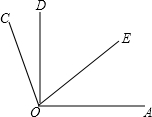 如图,OE为∠AOD的平分线,∠COD=
如图,OE为∠AOD的平分线,∠COD= 如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,∠EOD=26°,则∠AOC=
如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,∠EOD=26°,则∠AOC=